Solving a Problem with an Easier Way: Moving the Origin

[ChiralSuperfields]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

The solution is

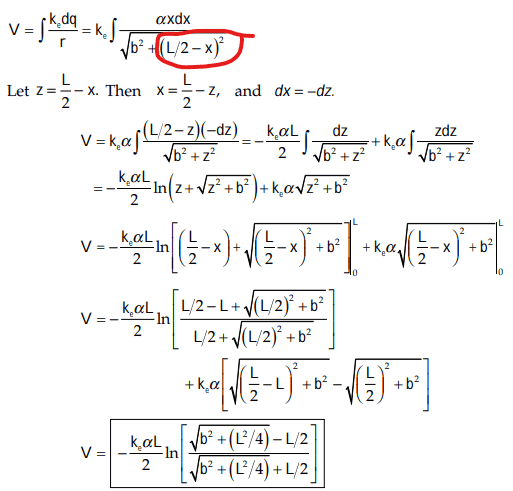
However could the bracket circled in red also be $(x - \frac {L} {2})^{2}$ since the terms are squared? Also if anyone else knows a simpler way to solve this problem please let me know.

I though an easier way to solve this problem would be moving the origin such that it is in the middle of the rod then:

$dV = \frac {k_e dx} {x}$ Then integrate over rod from $\frac {-L} {2}$ to $\frac {L} {2}$ to get:

$V = k_e\log_eL$ since $-In(-L)$ is undefined. I guess the authors must of knew this and decided to have the origin at the left of the rod. Anybody else agree with that?

Many thanks!

 

[kuruman]

However could the bracket circled in red also be $(x - \frac {L} {2})^{2}$ since the terms are squared?

Yes, it is true that $(L/2-x)^2=(x-L/2)^2.$ Check it out for yourself just be expanding the squares algebraically.

I though an easier way to solve this problem would be moving the origin such that it is in the middle of the rod then:

$dV = \frac {k_e dx} {x}$ Then integrate over rod from $\frac {-L} {2}$ to $\frac {L} {2}$ to get:

$V = k_e\log_eL$ since $-In(-L)$ is undefined. I guess the authors must of knew this and decided to have the origin at the left of the rod. Anybody else agree with that?

Many thanks!

I disagree with that. You wrote $dV = \frac {k_e dx} {x} .$ The denominator should be the distance from a point at distance $x$ from the midpoint of the rod to point B on the y-axis. What is that distance according to the Pythagorean theorem?

 

[ChiralSuperfields]

Yes, it is true that $(L/2-x)^2=(x-L/2)^2.$ Check it out for yourself just be expanding the squares algebraically.

Thank you for your reply @kuruman ! Ahh, I see - expanding is good way to prove that they are indeed equal!

I disagree with that. You wrote $dV = \frac {k_e dx} {x} .$ The denominator should be the distance from a point at distance $x$ from the midpoint of the rod to point B on the y-axis. What is that distance according to the Pythagorean theorem?

Oh I see my error the denominator should be $(x^2 + b^2)^{1/2}$ since I am finding the potential at a point above the rod. However, are we allowed to solve this problem this way since they defined the origin to the left of the rod not the middle?

Many thanks!

 

[kuruman]

If the origin is given to you by the problem, it is a good idea not to move it because the expected solution is relative to the given origin.

On edit: See post #6 and sorry for the mess.

 

[ChiralSuperfields]

If the origin is given to you by the problem, it is a good idea not to move it because the expected solution is relative to the given origin.

Got it, thank you for your help @kuruman !

 

[kuruman]

Got it, thank you for your help @kuruman !

Sorry, I take it back. For calculating the electrostatic potential relative to infinity at a specific point, the choice of origin doesn't matter. I was thinking of the electrostatic potential function $V(x,y,z)$. That is not what this problem is asking.

 

[ChiralSuperfields]

Sorry, I take it back. For calculating the electrostatic potential relative to infinity at a specific point, the choice of origin doesn't matter. I was thinking of the electrostatic potential function $V(x,y,z)$. That is not what this problem is asking.

Thanks for your reply @kuruman ! I did not know that. However, given that is the case then why cannot not get the same result as the solutions using this integration over the rod

$dV = \frac {k_e dx} {(x^2 + b^2)^{1/2}}$?

Many thanks!

 

[haruspex]

Thanks for your reply @kuruman ! I did not know that. However, given that is the case then why cannot not get the same result as the solutions using this integration over the rod

$dV = \frac {k_e dx} {(x^2 + b^2)^{1/2}}$?

Many thanks!

Because you dropped the x in the numerator.

 

[ChiralSuperfields]

Because you dropped the x in the numerator.

Thank you @haruspex ! Looks like I also dropped the alpha too!

$dV = \frac {k_e αx dx} {(x^2 + b^2)^{1/2}}$

Which I will try to integrate over the rod.

Many thanks!

 

[nasu]

What quantity is labeled with $\alpha$ in this problem? There is no mention of it in the OP.

 

[SammyS]

Thank you @haruspex ! Looks like I also dropped the alpha too!

$dV = \frac {k_e αx dx} {(x^2 + b^2)^{1/2}}$

Which I will try to integrate over the rod.

Many thanks!

We were not given a complete statement of the problem. we were only given the following, plus the published solution.

In looking at the solution, it's apparent that linear charge density, $\lambda$, is not constant, but is linear function, going from $0$ at the left end of the rod, to $\alpha L$ at the right end of the rod. As the rod is pictured, lying along the positive x-axis, with one end at the origin, the charge density is given by: $\lambda =\alpha x$ .

If you move the rod to the left, so that it is centered at the origin, you will need to alter the form of the charge density so that it still goes from $0$ at the left end of the rod, to $\alpha L$ at the right end of the rod. That is to say, $\lambda$ will then be given as:

$\displaystyle \quad\quad\quad \lambda =\alpha\left(x+\dfrac{L}{2}\right)$

Therefore, you will need to integrate the following over the length of the rod.

$\displaystyle \quad\quad\quad dV =k_e \dfrac { \alpha\left(x+L/2\right) dx} {(x^2 + b^2)^{1/2}}$

 

[ChiralSuperfields]

What quantity is labeled with $\alpha$ in this problem? There is no mention of it in the OP.

Thanks for your reply @nasu ! Sorry it was in the problem above

 

[ChiralSuperfields]

We were not given a complete statement of the problem. we were only given the following, plus the published solution.
View attachment 321181
In looking at the solution, it's apparent that linear charge density, $\lambda$, is not constant, but is linear function, going from $0$ at the left end of the rod, to $\alpha L$ at the right end of the rod. As the rod is pictured, lying along the positive x-axis, with one end at the origin, the charge density is given by: $\lambda =\alpha x$ .

If you move the rod to the left, so that it is centered at the origin, you will need to alter the form of the charge density so that it still goes from $0$ at the left end of the rod, to $\alpha L$ at the right end of the rod. That is to say, $\lambda$ will then be given as:

$\displaystyle \quad\quad\quad \lambda =\alpha\left(x+\dfrac{L}{2}\right)$

Therefore, you will need to integrate the following over the length of the rod.

$\displaystyle \quad\quad\quad dV =k_e \dfrac { \alpha\left(x+L/2\right) dx} {(x^2 + b^2)^{1/2}}$

Thank you very much for your reply @SammyS , that is very helpful!

 

[ChiralSuperfields]

Sorry, I take it back. For calculating the electrostatic potential relative to infinity at a specific point, the choice of origin doesn't matter. I was thinking of the electrostatic potential function $V(x,y,z)$. That is not what this problem is asking.

Thank you for your reply @kuruman !

Why does it not matter where we choose to put the origin for calculating the electrostatic potential at a specific point? I understand that the electrostatic potential is calculated relative to zero potential at infinity.

Is that the only reason? I guess it makes sense since no matter where we choose to put the origin, the zero potential will be infinitely far away every time we choose a new origin.

Thank you!