Solving a Tricky Tension Problem on a Moving Train

[stateofdogma]

Homework Statement

A bored but observant child on a moving train ties a ball to one end of a string and ties the other end to a light fixture on the ceiling of the train. When the train slows down, the child notices that the string is no longer hanging straight down but instead makes an angle of 19 degrees with the vertical. The mass of the ball 175g.

a) will the string tilt forward or backward? Find the acceleration of the train.

b) What is the tension in the string?

Homework Equations

F=ma

The Attempt at a Solution

Sadly although this question had a complete solution i did not understand it.
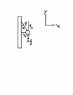
First the drawing in the textbook made no sense.(I've provided I file below)
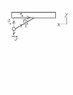
This is my FBD( second in attachments)

these are my equations

F_y = -T\sin\theta - mg = ma_y
F_x= -T\cos\theta = -ma_x

I didn't get far in trying to reduce, the solution in the book is acceleration 3.38m per second squared and the tension is 1.82 N.

 

[Chestermiller]

Your force balance in the y-direction is incorrect. The T term and the mg term should have opposite signs. Also, what is your understanding of what the acceleration in the y direction is? Also, your FBD diagram shows that the angle of the string with the horizontal is 19 degrees, rather than with the vertical. Use the y force balance to solve for the tension T.

Chet

 

[stateofdogma]

I see my mistake on the y axis( that was a typo) but are you saying that the Fy is equal to mg by Newtons third law and then that Fx is equal to the (acceleration of the train) and the mass of the ball. And thanks that's quite illuminating