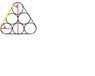
SUMMARY
The discussion focuses on solving a trigonometric word problem involving the calculation of the length of a metal band that encircles six identical pipes, each with a radius of 1 foot. The user proposes a strategy that includes dividing the figure in half, calculating the lengths of two arcs, and determining the length of a yellow line that connects the arcs. The user suggests that the angle x is 30 degrees and emphasizes the importance of using cosine and sine functions to find the lengths of the curved and straight segments of the band.
PREREQUISITES
- Understanding of basic trigonometric functions (sine and cosine)
- Familiarity with arc length calculations in circles
- Knowledge of geometric properties of circles and angles
- Ability to visualize and manipulate geometric figures
NEXT STEPS
- Study arc length formulas in circular geometry
- Learn about the properties of angles in polygons
- Explore the application of trigonometric functions in real-world problems
- Practice solving similar trigonometric word problems
USEFUL FOR
Students studying trigonometry, educators teaching geometric concepts, and anyone interested in applying trigonometric principles to solve practical problems.