Trig Word Problem: Finding Height of a Baloon

[Williams.235]

Homework Statement

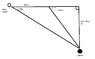
While taking a ride in a hot-air balloon, Fran wonders how high he is. To find out, he chooses a landmark that is to the east of the balloon and measures the angle of depression to be 54 degrees. A few minuets later, after traveling 100 feet east, the angle of depression to the same landmark is determined to be 61 degrees. Use this information to determine the height of the balloon.

Homework Equations

Standard Trig Identities

The Attempt at a Solution

I have a firm grasp of the material in general but am struggeling with properly sketching the problem. I have attatched my representation of the problem in picture form. My problem is that we have only studied right triangle trig (2 weeks into course) so my value of 100 feet has to, in some way, be associated with the right triangle portion of the drawing. I went ahead a solved the problem assuming i can use the 100 feet in the right triangle portion of the drawling: my work is below:

Tan 61 degrees = H/100ft

(100ft)(Tan 61 degrees)= H

Answer: Approx. 180.41 feet.

I am not sure if it is right, if it is then I still don't quite understand how to visualize the problem. What do you guys think?

 

[tiny-tim]

Hi Williams.235!

… am struggeling with properly sketching the problem …
…
Tan 61 degrees = H/100ft

Nooo … 100 isn't part of the triangle, is it?

General tip: half the job of a sketch is to give letters to anything that's important … without a letter, you can't talk about it!

in this case, call the bit to the right of the 100 feet "x", and carry on from there.

 

[Williams.235]

Hi Williams.235!


Nooo … 100 isn't part of the triangle, is it?

General tip: half the job of a sketch is to give letters to anything that's important … without a letter, you can't talk about it!

in this case, call the bit to the right of the 100 feet "x", and carry on from there.

If I do that, I get

tan 61 degrees = H/x

I am left with an unknown equaling an unknown.

When I look at the overall triangle, I tried to compute:

Tan 54 degrees = H/100+x
(100+X) Tan 54 degrees = H
137.64 + 1.38X = H

Then, I attempted to take Tan 61 degrees = x/(137.64 +1.38X) and received a negative value for X, which would mean the distance from the balloon to the landmark is negative which is not possible.

 

[tiny-tim]

tan 61 degrees = H/x
…
Tan 54 degrees = H/100+x
(100+X) Tan 54 degrees = H
137.64 + 1.38X = H
…
Tan 61 degrees = x/(137.64 +1.38X) …

No, that's the wrong way up!

(but anyway, it would be easier to equate the two values of H )

 

[HallsofIvy]

Another way to do this: Looking at the obtuse triangle on the left, you know that one angle is 54 degrees and another is 180- 61= 119 degrees. The third angle, at the base, is 180- 54- 119= 7 degrees (also 61- 54 degrees, of course).

You can use the sine law, then, to find the length of that line between "64 degrees" and "landmark" (another good reason to label the sides!), the hypotenuse of the small right triangle, and then use sin(61) to find the height of the balloon.