Solving for Derivative of 2x^3-x^2+cx+d

  • Context: MHB 
  • Thread starter Thread starter Chipset3600
  • Start date Start date
  • Tags Tags
    Derivative
Click For Summary
SUMMARY

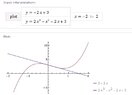
The discussion focuses on finding the derivative of the cubic function y = 2x^3 - x^2 + cx + d, given that the line 2y + 4x - 6 = 0 is tangent to the curve. The derivative is calculated as y' = -12x^2 + 2x - 2. By equating this derivative to the slope of the tangent line (-2), participants derive two x-values, which are then used to express c and d. The final values determined are c = -2 and d = 3, with the tangent point identified as (0, 3).

PREREQUISITES
  • Understanding of calculus, specifically derivatives and tangent lines.
  • Familiarity with cubic functions and their properties.
  • Ability to solve equations involving multiple variables.
  • Knowledge of implicit functions and their applications.
NEXT STEPS
  • Study the concept of derivatives in calculus, focusing on polynomial functions.
  • Learn about tangent lines and their geometric significance in calculus.
  • Explore implicit differentiation and its applications in finding derivatives.
  • Practice solving cubic equations and determining their critical points.
USEFUL FOR

Students studying calculus, mathematics educators, and anyone interested in understanding the relationship between derivatives and tangent lines in polynomial functions.

Chipset3600
Messages
79
Reaction score
0
Hello MHB, please help me solve this problemn.

knowing that 2y+4x-6=0 is the equation which is one of the lines tangent to the curve y= 2x^3-x^2+cx+d.
Find the derivative of this function in one of the points of the curve.
 
Physics news on Phys.org
What do you require of the derivative and the curve so that the given line is tangent to the curve?
 
MarkFL said:
What do you require of the derivative and the curve so that the given line is tangent to the curve?
this implicit function "2y+4x-6=0" is tangent of this curve "y= 2x^3-x^2+cx+d"
the gradient is "-2", but i don't know my C and D. How can i find the common point?
 
Equate the derivative of the cubic to -2, and you may express c as a function of x.

Then, substitute for c into the cubic and find where this new function's derivative is equal to -2. You will get 2 x-values. One of these will allow you to then easily find c and d.
 
MarkFL said:
Equate the derivative of the cubic to -2, and you may express c as a function of x.

Then, substitute for c into the cubic and find where this new function's derivative is equal to -2. You will get 2 x-values. One of these will allow you to then easily find c and d.

Lets see if i understood: View attachment 453

Is this what you mean??
 

Attachments

  • load.jpg
    load.jpg
    30.4 KB · Views: 71
Yes, after substituting for c, then taking the derivative, you have found:

$\displaystyle y'=-12x^2+2x-2$

Now, equate this to -2, and you will have 2 roots, one of which allows you to find by substitution into the original cubic and tangent line the value of d (when you equate the two as they must have the same value where they touch) and then use the x-value also in your expression for c to find its value.
 
MarkFL said:
Yes, after substituting for c, then taking the derivative, you have found:

$\displaystyle y'=-12x^2+2x-2$

Now, equate this to -2, and you will have 2 roots, one of which allows you to find by substitution into the original cubic and tangent line the value of d (when you equate the two as they must have the same value where they touch) and then use the x-value also in your expression for c to find its value.

My teacher said that this is just an exercise concept.
knowing that the derivative in point is the gradient of the tangent line
And he give the equation("2y+4x-6=0") of one of tangent line in some point.
The answer is: m(x)= -2...
 
I assumed your teacher wanted you to find a tangent point (0,3), and the values of c and d, which are -2 and 3 respectively.

Here is a plot:
 

Attachments

  • cubicandtangent.jpg
    cubicandtangent.jpg
    11.3 KB · Views: 67
MarkFL said:
I assumed your teacher wanted you to find a tangent point (0,3), and the values of c and d, which are -2 and 3 respectively.

Here is a plot:

Every body thought that, thanks for the help MarkFL.
 
  • #10
Glad to help, I found the problem to be interesting, even if I did interpret it incorrectly! :)
 

Similar threads

Undergrad Partial derivatives of the function f(x,y)
  • · Replies 6 ·
Replies
6
Views
3K
MHB Q1 Can you pass this 3 question AP calculus Quiz in 10 minutes
  • · Replies 3 ·
Replies
3
Views
1K
MHB How to Perform Implicit Differentiation on \(x^2-4xy+y^2=4\)?
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad Different Substitution for Solving an Integral
  • · Replies 6 ·
Replies
6
Views
2K
High School Confusion on Implicit Differentiation
  • · Replies 16 ·
Replies
16
Views
3K
MHB How to Find the Second Derivative with Given Equation at a Specific Point?
  • · Replies 1 ·
Replies
1
Views
1K
MHB Find the equation of the tangent and normal to.
  • · Replies 4 ·
Replies
4
Views
2K
MHB Solving for d^2y/dt^2: Finding d^2y/dt^2 with dx/dt=1/2
  • · Replies 1 ·
Replies
1
Views
4K
MHB How Does the Derivative of a Cubic Function Result in a Tangent Line?
  • · Replies 4 ·
Replies
4
Views
3K
MHB Finding k for x is undefined at $x=2$
  • · Replies 3 ·
Replies
3
Views
1K