Solving for L in Tunneling Probability Equation

[Kaldanis]

I'm in the process of studying for my final and I just can't solve this problem:

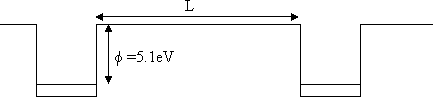
The work function (energy needed to remove an electron) of gold is 5.1 eV. Two pieces of gold (at the same potential) are separated by a distance L.

For what value of L will the transmission probability for an electron to cross from one to the other be T ≈ 10-3? Assume that G = 1 in the formula for the tunneling probability.

(a) L = 0.001 nm
(b) L = 0.02 nm
(c) L = 0.1 nm
(d) L = 0.3 nm
(e) L = 4

The attempt at a solution

I'm pretty sure I rearrange the tunneling equation and solve for L. Things are made easier since I'm told G=1. This means that L = -\frac{ln(T)}{2K} , where K=\sqrt{\frac{2m}{\hbar}(U_{0-E})}. My only problem is which values do I use for U₀ and E?

 

[PhysicsGente]

E is total energy and V is potential energy. Oh, and think about the definition of the work function ;).

 

[Kaldanis]

I'm still not having any luck with this problem. I know that I need to find the Potential Energy (U₀) and total Energy. The work function is given as 5.1eV and from the picture it looks like this is the value of the PE, I think I could be wrong though. I still have no idea how to find potential and total from only the work function.

My final for quantum is tomorrow, can anyone help clear this up for me?

 

[Kaldanis]

Nevermind, I got it. :)

 

[tarunnurat]

How did you do it? I have my final in a few hours and it would be nice to know.