Solving for Pendulum Bob's d from Length L

[auk411]

Homework Statement

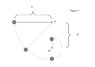
Figure 2 shows a pendulum with a point-like pendulum bob on a string with a length = L fixedly attached to a support so as to form a friction-less pivot-point P. The bob is released at rest from the height of the pivot point. The bob swings to its lowest point where upon the string makes contact with a very thin horizontal bar positioned a distance d below the pivot point of the pendulum. The bob continues traveling past its lowest point with a new pivot point P’ and reduced radius of curvature and is barely able to travel to the top of the bar in a circular path. Find a very simple expression for d in terms of L.

see attachment

Homework Equations

Work done by gravity = mgh

Radius of smaller circle = L -D

Fnet = T - mg = mv^2/r

The Attempt at a Solution

?

someone at least show me how I'm supposed to be setting this up.

 

[tiny-tim]

welcome to pf!

hi auk411! welcome to pf!

hint: the tension at the end is zero, so if the speed at the bottom is v, what is the speed at the end?

(btw, do you still need help on your other thread?)

 

[auk411]

hi auk411! welcome to pf!

hint: the tension at the end is zero, so if the speed at the bottom is v, what is the speed at the end?

(btw, do you still need help on your other thread?)

I get v^2 = g(L-D).

I then go on to say that mgL = .5m(v^2) - mg2(L-D).
= .5m(g)(L-D) - 2mg(L-D)
Reducing leads to L = .5(L-D) - 2 (L-D), which equals:
2L = L - D - 4(L-D).
2L = L -D -4L + 4D
2L = -3L + 3D
5L = 3D
(5/3)L=D

This is false. For D is shorter than L.

What gives?

I'm pretty sure the answer is D = (3/5)(L)

Also, I assume that y = 0 is directly below the starting position. So the y position of the first position of the bob is y = L.
B) No, I don't need help on the other thread. Thanks!

 

[tiny-tim]

hi auk411!

(just go up :zzz: …)

(oh, and try using the X² icon just above the Reply box )

I then go on to say that mgL = .5m(v^2) - mg2(L-D).

ooh, your proof was fine, except that you screwed it up at the start with this line …

try it with a + instead of a -

 

[auk411]

hi


ooh, your proof was fine, except that you screwed it up at the start with this line …

try it with a + instead of a -

Could you say WHY this is the case? I was under the impression that one of them had to be negative.

 

[tiny-tim]

Could you say WHY this is the case? I was under the impression that one of them had to be negative.

Yes, but you've put it on the wrong side of the equation.

What matters is the difference in height, which is L - 2r, = L - 2(L - D).