nDever
- 76
- 1
I'm working on the physics engine component of a game engine I'm building, and I need some guidance with this particular situation.
Consider a square with mass M that is free to translate in the xy plane and free to rotate about any axis perpendicular to the page (Fig. 1)
If a linear impulse J is applied at a point above the center of mass (CM) as shown below, I know there must be some angular impulse (momentary torque) generated since there is a component of J that is perpendicular to the displacement vector from CM. I imagine this angular impulse will tend to rotate the square clockwise.
However, I can also imagine that the CM will also undergo translation since the square is not constrained. How would I go about computing the overall rotational + translational motion of this system?
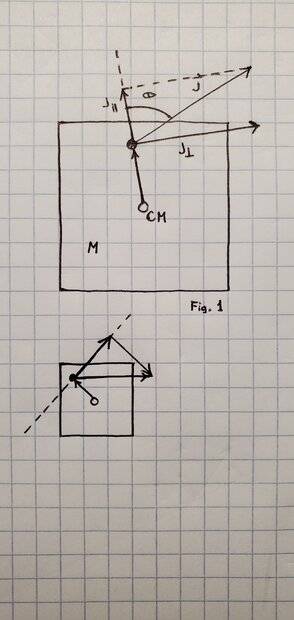
Consider a square with mass M that is free to translate in the xy plane and free to rotate about any axis perpendicular to the page (Fig. 1)
If a linear impulse J is applied at a point above the center of mass (CM) as shown below, I know there must be some angular impulse (momentary torque) generated since there is a component of J that is perpendicular to the displacement vector from CM. I imagine this angular impulse will tend to rotate the square clockwise.
However, I can also imagine that the CM will also undergo translation since the square is not constrained. How would I go about computing the overall rotational + translational motion of this system?