SUMMARY
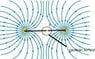
The discussion centers on the application of Gauss's Law to a system of two point charges, +q and +q, separated by a distance d. It is established that at a point P, located at d/2 from one charge, the electric field cancels out due to symmetry. However, the surface integral of the electric displacement field (D) over a Gaussian surface enclosing both charges yields a non-zero value of 2q. The conversation emphasizes the importance of the chosen Gaussian surface and the necessity of performing the mathematical calculations to validate the arguments presented.
PREREQUISITES
- Understanding of Gauss's Law and its mathematical formulation.
- Familiarity with electric field concepts and point charge behavior.
- Knowledge of surface integrals in electromagnetism.
- Ability to visualize and analyze cylindrical symmetry in electric fields.
NEXT STEPS
- Study the mathematical derivation of Gauss's Law for different charge configurations.
- Learn how to compute electric field lines and their implications in electrostatics.
- Explore the concept of electric flux and its calculation through various Gaussian surfaces.
- Investigate the behavior of test charges in electric fields and the concept of stable vs. unstable equilibrium points.
USEFUL FOR
Students of physics, particularly those focusing on electromagnetism, educators teaching Gauss's Law, and anyone interested in advanced electrostatics concepts.