Solving Giant Swing Horizontal Cable Tension

[jasonchiang97]

1. Homework Statement
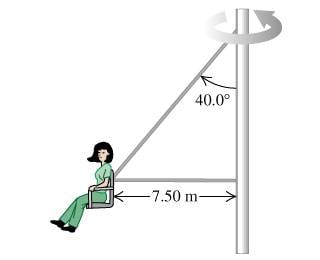
In one of the versions of the "Giant Swing", the seat is connected to two cables, one of which is horizontal (Figure 1) . The seat swings in a horizontal circle at a rate of 33.0 rev/min .

If the seat weighs 295 N and a 869-N person is sitting in it, find the tension in the horizontal cable.

Homework Equations

F_c=mv²/r
Period=circumference/velocity so 2πR/v

The Attempt at a Solution

I drew two FBD(free body diagrams). One for the person and one for the chair
For the person : TsinΘ-W-Fn=0
T=(W+Fn)/sinΘ
Fn = Weight of the chair

For the chair: T_h+TcosΘ=mv²/r
T_h = mv²/r - TcosΘ
mv²/r - [(W_c + W_p)/sinΘ]*cosΘ

To get the velocity, we use period = circumference /velocity
33 rev/min * 1min/60 sec = 0.55 rev/sec
0.55 = 2π(7.5)/v
v=85.68m/s
m= (W_p + W_c)/9.8
So (W_p+W_c/9.8)(81.68)²/7.5 - (295+869)/tan40

Basically I end up getting a huge number and I'm fairly certain that it's wrong but can't see why

 

[Nathanael]

I drew two FBD(free body diagrams). One for the person and one for the chair

I haven't checked your work in detail (sorry) but you should be able to treat the person and chair as a single object. The vertical component of the tension in the slanted cable must balance the weight of the person+chair, and the horizontal components of the two tensions must provide the centripetal acceleration.

 

[jasonchiang97]

I haven't checked your work in detail (sorry) but you should be able to treat the person and chair as a single object. The vertical component of the tension in the slanted cable must balance the weight of the person+chair, and the horizontal components of the two tensions must provide the centripetal acceleration.

yea that's basically what I did. I guess my main problem is I don't know how to convert rev/min to m/s so I just took the rev/min and divided it by 60 to get rev/sec which gives 0.55rev/sec

I then took 2π(7.5)/0.55 to get velocity. Wondering if that step is correct

 

[Nathanael]

$2\pi\frac{\text{radians}}{\text{revolution}}\cdot 7.5\frac{\text{meters}}{\text{radian}}\cdot\frac{1}{0.55\frac{\text{revolutions}}{\text{second}}}$

Check the units in the above equation. If it is not meters/second then try to fix it so it is.