- #1
Arejang
- 32
- 0
[SOLVED] Dynamics of Circular Revolution
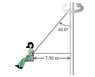
In another version of the "Giant Swing", the seat is connected to two cables as shown in the figure View Figure , one of which is horizontal. The seat swings in a horizontal circle at a rate of 33.1 rev/min
If the seat weighs 252 N and a 831 N person is sitting in it, find the tension in the horizontal cable.
If the seat weighs 252 N and a 831 N person is sitting in it, find the tension in the inclined cable.
If I read the problem right, this should be the formula used
(4pi^2*R)/T^2
I first found the a_rad by plugging in 7.5m for R and 60sec/33.1rev for T. Afterwards, I convert the given Newtons of the chair and the person from problem to kilograms by dividing by 9.8 m/s^2. Once I calculated the mass of both person and chair, I added them together and multiplied by my acceleration from earlier to get the amount of Newtons for the tensions for the cables. A big question is, I'm pretty sure trig absolutely must play a role in it due to the angle of 40 degrees given, but I'm not sure whether it should be 7.5*sin(theta) or 7.5*cos(theta).
In short, what I did was this:
(4pi^2*7.5*sin(40))/(60/33.1)^2
Before I did anything with this resultant acceleration, I first added two weights of the seat and the person. Then I divided the sum by 9.8 m/s^2 to get the mass in kilograms. Then I multiplied the resultant kilograms to the acceleration I calculated from above to get 64000 N. This was for the horizontal tension on the cable. Please let me know if I had done anything wrong. Thanks!
Homework Statement
In another version of the "Giant Swing", the seat is connected to two cables as shown in the figure View Figure , one of which is horizontal. The seat swings in a horizontal circle at a rate of 33.1 rev/min
If the seat weighs 252 N and a 831 N person is sitting in it, find the tension in the horizontal cable.
If the seat weighs 252 N and a 831 N person is sitting in it, find the tension in the inclined cable.
Homework Equations
If I read the problem right, this should be the formula used
(4pi^2*R)/T^2
The Attempt at a Solution
I first found the a_rad by plugging in 7.5m for R and 60sec/33.1rev for T. Afterwards, I convert the given Newtons of the chair and the person from problem to kilograms by dividing by 9.8 m/s^2. Once I calculated the mass of both person and chair, I added them together and multiplied by my acceleration from earlier to get the amount of Newtons for the tensions for the cables. A big question is, I'm pretty sure trig absolutely must play a role in it due to the angle of 40 degrees given, but I'm not sure whether it should be 7.5*sin(theta) or 7.5*cos(theta).
In short, what I did was this:
(4pi^2*7.5*sin(40))/(60/33.1)^2
Before I did anything with this resultant acceleration, I first added two weights of the seat and the person. Then I divided the sum by 9.8 m/s^2 to get the mass in kilograms. Then I multiplied the resultant kilograms to the acceleration I calculated from above to get 64000 N. This was for the horizontal tension on the cable. Please let me know if I had done anything wrong. Thanks!
Attachments
Last edited: