Solving Horizontal Force of Screw on Shelf Bracket

[Jacob87411]

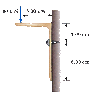
A shelf bracket is mounted on a vertical wall by a single screw, as shown in Figure P12.59. Neglecting the weight of the bracket, find the horizontal component of the force that the screw exerts on the bracket when an F = 86.0 N vertical force is applied as shown.

Ok so we have three equations like usual with statics.

Forces in Y = 86N-Fb=ma
Forces in X = 0=ma
Torque=0 so (86)(.05)-(Fb)(.03)=0
Taking the point of rotation at the top right corner of the bracket, 3cm above the screw.
Fb=Force of the bracket

Or do you solve for Fb in the torque equation giving Fb=143.33 then find its X and Y components. The Y would be 86, then the X would be 57.33?

I guess what I am confused by is why there is an X force from the screw and how to find it

 

[vaishakh]

On what axis will the object rotate? How do we measure torque? I would appeal for a bit more clearer information of the question.

 

[Jacob87411]

Thats all that is given, the diagram and that question. If its assumed it doesn't rotate the force being applied is pushing it counterclockwise so the bracket must hold it thus pushing clockwise?

 

[Gladi8or2]

Taking a quick look at the picture, I'd say there are two reaction forces: one at the screw and one at the lowest point of the bracket. Both reaction forces have a horizontal and a vertical component, so we have four unknown values. We also have four equations:

1 horizontal force equation (which will tell you the horizontal forces in the two reaction points are equal in size but opposite in direction)
1 vertical force equation
1 horizontal torque equation
1 vertical torque equation

I suggest to take the torque around the lowest point of the bracket, cause that's where the bracket will rotate.

And by the way, why do you use the term ma in your equations? You don't have to know anything about the acceleration or so. You also have no information about mass or something.

 

[Jacob87411]

Ok that makes sense but is this how some of the equations are set up...The force from the screw should be opposing the 86N force, right? Is the bottom of the bracket also opposing the 86N force?

 

[Doc Al]

Do exactly what Gladi8or2 suggested in his last post:

I suggest to take the torque around the lowest point of the bracket, cause that's where the bracket will rotate.

That's all you need to do. One equation and you'll have your answer.

 

[Jacob87411]

Torque around the bottom would equal 0 since it doesn't rotate so:

0=(86)(.05)-(.06)(Fb)?

 

[Doc Al]

If Fb refers to the horizontal force of the screw on the bracket, then that is correct.