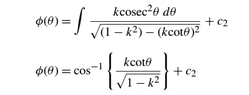The discussion focuses on solving a specific integral using trigonometric substitution. Participants explore whether the denominator should be $(1-k^2)$ or $(1-k^2)^2$ and suggest various substitutions, including $k \cot(\theta)$ and $\cot(\theta)=\frac{\sqrt{1-k^2}}{k}\cos(u)$. One user reports successfully solving the integral but arrives at a result involving arcsin instead of arccos, prompting a discussion about the validity of both forms due to the identity relating sine and cosine inverses. The conversation emphasizes the flexibility of integral solutions and the importance of understanding trigonometric identities in calculus.