Solving Laplace Equations using this boundary conditions?

[astrodeva]

The equation is Uxx + Uyy = 0
And domain of solution is 0 < x < a, 0 < y < b
Boundary conditions:
Ux(0,y) = Ux(a,y) = 0
U(x,0) = 1
U(x,b) = 2

What I've done is that I did separation of variables:
U(x,y)=X(x)Y(y)

Plugging into the equation gives:
X''Y + XY'' = 0

Rearranging:
X''/X = -Y''/Y = k

For case k > 0, I saw that it gives no non-trivial solutions.
For case k = 0, I solved it and found U(x,y) = y/b + 1

For case k < 0, I'm slightly lost.
X'' + kX = 0
Y'' - kX = 0

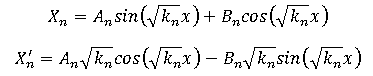
Using the X boundary conditions:

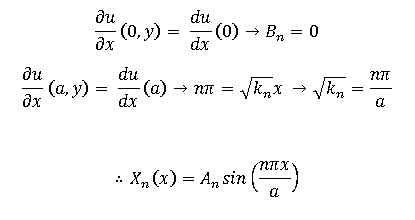
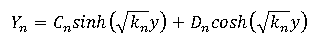
Using the Y boundary condition:

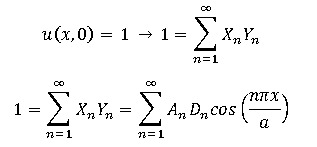
Using Fourier Series to find the coefficient:

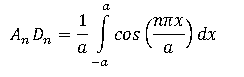
But the integral just gives Dn = 0, and this doesn't satisfy u(x,0) = 1.

Can someone explain where I went wrong?

Thanks!

 

[pasmith]

Your working is confusing.

If you start with X&#039;&#039; = kX and want k &lt; 0, you should then be writing \sin(\sqrt{|k|}x) and so forth, or defining k = -c^2 where c \geq 0.

You want to be using cosines, which in fact you end up doing, but only after expressly stating that X_n = A_n\sin(n\pi x/a).

Now the cosine expansion of 1 on [0,a] is \cos(0x). Thus you have correctly determined that all the other coefficients vanish.