Bman900
- 12
- 0
Now I solved something similar to this problem yesterday (https://www.physicsforums.com/showthread.php?t=447168) thanks to the help of p21bass but this one is really out there and I have no idea where to begin.
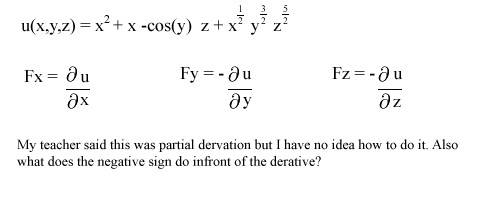
I don't know where to even start as this is my first time ever seeing this problem. Where should I start?
Homework Statement
Homework Equations
The Attempt at a Solution
I don't know where to even start as this is my first time ever seeing this problem. Where should I start?