Acceleration and distance using derivatives.

Click For Summary
SUMMARY

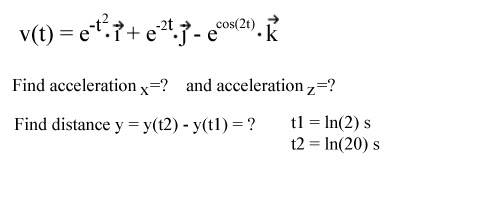
The discussion focuses on the relationship between derivatives and integrals in the context of acceleration and distance. Participants confirm that the correct approach involves using the chain rule for differentiation and substitution for integration. Specifically, the integration of e^u is highlighted, along with the importance of correctly applying the negative sign in trigonometric derivatives. The conversation emphasizes the need for proper differentiation and integration techniques to solve related physics problems.

PREREQUISITES
  • Understanding of basic calculus concepts, including derivatives and integrals.
  • Familiarity with the chain rule in differentiation.
  • Knowledge of integration techniques, particularly substitution.
  • Basic trigonometric derivatives, such as the derivative of cosine.
NEXT STEPS
  • Study the chain rule in more depth, focusing on complex functions.
  • Learn integration techniques, specifically the substitution method.
  • Review the properties and applications of exponential functions, particularly e^x.
  • Explore trigonometric derivatives and their applications in calculus.
USEFUL FOR

Students studying calculus, particularly those tackling physics problems involving motion, as well as educators looking for examples of derivative and integral applications.

Bman900
Messages
12
Reaction score
0
Now I understand the basic concept that if one derivative's velocity you get acceleration and if you integrate velocity you will get the distance. But what about in this case?

Homework Statement


problem1.jpg

Homework Equations


The Attempt at a Solution


attemptedsolution-1.jpg
 
Physics news on Phys.org
You didn't differentiate properly. You need the chain rule(s).

So, I'm thinking you probably didn't integrate correctly, either.

But, we don't know, as you didn't post your results.
 
Well I didn't get to that yet because I was not sure that is the correct way of finding the answers. So am I at least derivating the right parts of the equation?
 
For what the problem is asking, yes - that's the correct approach.
 
Ok so I derivated but I could not integrate because I have only know e^x. Am looking into to solving that but please tell me if the answers so far are correct?

attemptedsolution-2.jpg
 
The a_x is correct, but not a_z. What is the derivative of cos?

And for the integration, set -2t to u, so that you integrate e^u. Don't forget that you are now integrating with respect to u!
 
Oh its -sin so the negative signs cancel out! Thanks. Am am about solve the integral here soon as I have to learn a bit more about the substitution method.
 
Am I correct?

integrate.jpg
 
Looks good to me!
 

Similar threads

Relating acceleration to distance and time
  • · Replies 5 ·
Replies
5
Views
3K
Displacement given the acceleration
  • · Replies 8 ·
Replies
8
Views
1K
How to Apply Derivatives in Physics Problems?
  • · Replies 9 ·
Replies
9
Views
1K
Solving for Work Done When Accelerating a Mass
  • · Replies 3 ·
Replies
3
Views
938
Dynamics of Circular Motion
  • · Replies 12 ·
Replies
12
Views
998
Deriving the particle's motion using numerical integration
  • · Replies 5 ·
Replies
5
Views
848
Derivation of an expression for centripetal acceleration
  • · Replies 3 ·
Replies
3
Views
2K
Find the acceleration in circular motion
  • · Replies 6 ·
Replies
6
Views
2K
Acceleration of a shot put ball
  • · Replies 3 ·
Replies
3
Views
3K
Deriving an equation for the velocity of a particle
  • · Replies 1 ·
Replies
1
Views
1K