Solving Plane Displacement Using Radar Data

[Double D Edd]

Okay, this should really be a fairly easy problem and my work is below this question:

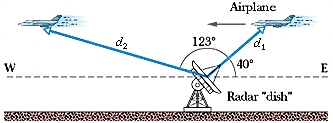
"A radar station detects an airplane approaching directly from the east. At first observation, the range to the plane is d1 = 384 m at 40° above the horizon. The airplane is tracked for another 123° in the vertical eastwest plane, the range at final contact being d2 = 770 m. Find the displacement of the airplane during the period of observation."

Heres what I did:

I first figured that the resultant R = d1-d2. So, I decided to break that into components.

Rx = d1x - d2x ; Ry = d1y - d2y. Now, to find the magnitude, I would take the square root of the sum of Rx^2 and Ry^2. And the direction would be the inverse tangent of Ry/Rx.

So, Rx = 384*cos(40) - (-770*Cos(57)). I took the other angle 180-123 = 57. So, Rx = 713.53m

Ry = 384*sin(40) - 770*sin(57). Ry = -398.94 (Which I think is totally wrong).

Now, the rest is pretty simple for me to do provided the above is correct, which I think is not.

I solved this and got the answer for the magnitude as 817.48m. Unfortunately, the answer is wrong.

Know what I am doing wrong here? Thanks :)

Edd.

 

[radou]

Take the triangle with sides d1, d2, and let's say d3, which is the displacement of the plane. The area of the triangle equals A = 0.5*d3*h (1), where h = d1*sin40. The area can be expressed as A=\frac{d_{1}^2 sin(123^{\circ}) sin \gamma}{2sin \alpha}, where \gamma is the angle between d1 and d3, and \alpha is the angle between d2 and d3. So, calculate the angles, get the area A, and you can get d3 from equation (1). I hope this works.