Homework Help Overview
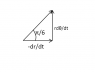
The discussion revolves around a problem involving three equal masses positioned at the vertices of an equilateral triangle, each moving towards the other with a constant speed. The objective is to determine the meeting point and time of convergence of the masses as they follow a specific motion rule.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Problem interpretation
Approaches and Questions Raised
- Participants explore the symmetry of the problem and its implications for the motion of the masses. Questions arise regarding how to mathematically represent the motion and the changing directions of the velocities. Some suggest using coordinate systems to facilitate the analysis.
Discussion Status
The discussion is active, with participants sharing insights about symmetry and coordinate systems. Some have begun to formulate equations for the positions and velocities of the masses, while others are considering the implications of using polar coordinates. There is no explicit consensus on the best approach yet, but several productive lines of inquiry are being pursued.
Contextual Notes
Participants note that the problem is not part of their formal coursework and was presented as a challenge. There is a mention of limited familiarity with cylindrical and polar coordinates among some participants, which may affect their approach to the problem.