Tangeton
- 62
- 0
Hello.
I find this whole topic of compound angle formula really confusing. I've been doing equations like cos(60+x) = sinx using the co function identities so far, yet this one seems to be impossible to do using cofunction identities so I need to know how to do it using compound angle formula. And yes this is definitely meant to be done using compound angle formula no double angle since in the book double angle hasnt even been mentioned at this point...
The question is to solve the equation 2sinx = 3cos(x-60) for values of x in the range 0 < x <180. I can't solve using cofunction due to the constants, but if anyone knows how to solve using cofunction identities with the constants this kind of answer is also welcomed.
I tried using compound angle formula after using cofunction identities where 2sinx = 2cos(90-x)
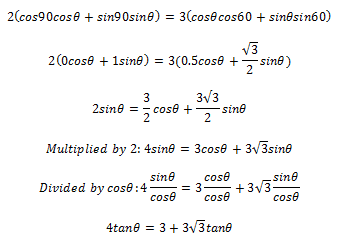
I tried to bring everything to the power of 2 but this gave me 11tan^2x = -9 so that is impossible.
I tried to take away 3sqrt3tan from 4tan which equaled 3 but this gave me the wrong answer.
The answer is 111.7.
Ive used x and feta interchangeably as don't know how to place feta symbol on keyboard.
Thanks for help.
EDIT 2: Corrected every typo eveywhere
I find this whole topic of compound angle formula really confusing. I've been doing equations like cos(60+x) = sinx using the co function identities so far, yet this one seems to be impossible to do using cofunction identities so I need to know how to do it using compound angle formula. And yes this is definitely meant to be done using compound angle formula no double angle since in the book double angle hasnt even been mentioned at this point...
The question is to solve the equation 2sinx = 3cos(x-60) for values of x in the range 0 < x <180. I can't solve using cofunction due to the constants, but if anyone knows how to solve using cofunction identities with the constants this kind of answer is also welcomed.
I tried using compound angle formula after using cofunction identities where 2sinx = 2cos(90-x)
I tried to bring everything to the power of 2 but this gave me 11tan^2x = -9 so that is impossible.
I tried to take away 3sqrt3tan from 4tan which equaled 3 but this gave me the wrong answer.
The answer is 111.7.
Ive used x and feta interchangeably as don't know how to place feta symbol on keyboard.
Thanks for help.
EDIT 2: Corrected every typo eveywhere
Last edited: