Moolisa
- 20
- 5
Summary: When ##V (x) = \frac 1 2 mω^2x^2 + mgx##
##H=\frac p 2m +V(x)##
Difficulty understanding how these change on variables came about
##y = x+\frac mg mω^2 = x+\frac g ω^2##
Apologies if this is not the appropriate thread. I chose this one because even though it's physics, I'm having issues with what seems to be basic math principles
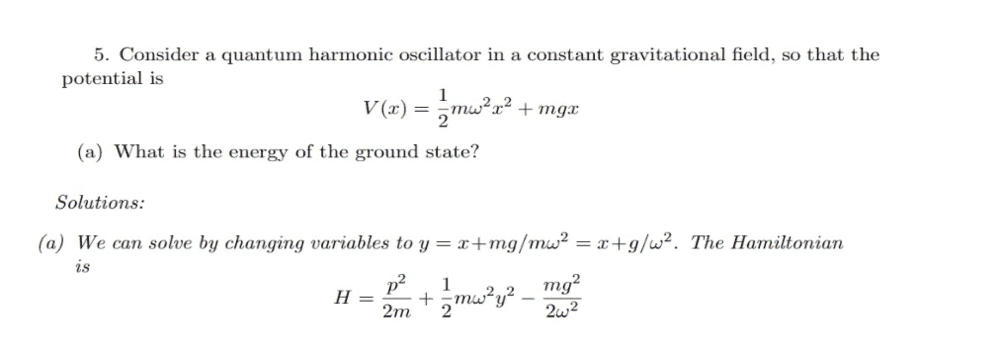
##V (x) = \frac 1 2 mω^2x^2 + mgx##
##y = x+\frac{mg} {mω^2} = x+\frac g ω^2##
So that
##H=\frac p {2m} +\frac 1 2 mω^2y^2 - \frac {mg^2} {2ω^2}##
I don't understand how the variables changed
By the way the solution looks like, I tried
##0= \frac 1 2 mω^2x^2 + mgx##
Rearranged so ##x=-\frac {2mg^2} {mω^2}##
But that is obviously not how to do it
Any help is appreciated, If you can, please tell me what this technique/concept this is, so I can read up on it. I looked up changing variables online but can only find the one for integrations, which I don't think is what this is
[Moderator's note: Moved from a technical forum and thus no template.]
##H=\frac p 2m +V(x)##
Difficulty understanding how these change on variables came about
##y = x+\frac mg mω^2 = x+\frac g ω^2##
Apologies if this is not the appropriate thread. I chose this one because even though it's physics, I'm having issues with what seems to be basic math principles
##V (x) = \frac 1 2 mω^2x^2 + mgx##
##y = x+\frac{mg} {mω^2} = x+\frac g ω^2##
So that
##H=\frac p {2m} +\frac 1 2 mω^2y^2 - \frac {mg^2} {2ω^2}##
I don't understand how the variables changed
By the way the solution looks like, I tried
##0= \frac 1 2 mω^2x^2 + mgx##
Rearranged so ##x=-\frac {2mg^2} {mω^2}##
But that is obviously not how to do it
Any help is appreciated, If you can, please tell me what this technique/concept this is, so I can read up on it. I looked up changing variables online but can only find the one for integrations, which I don't think is what this is
[Moderator's note: Moved from a technical forum and thus no template.]