Some help on a matrix question please.

  • MHB
  • Thread starter khehrap
  • Start date
  • Tags
    Matrix
In summary, the conversation is about the meaning of $A^T$ and finding the inverse of a matrix for solving a system of equations. The solution is to fill in the missing entries with 0's and use the correct values for calculations.
  • #1
khehrap
3
0
View attachment 2019
Hi. I am wondering if I can get some help on one or two questions on the sheet attached. I have worked out A^2B but am a bit puzzled on the meaning of A^TB. It is probably something very simple but I am struggling could someone help me possibly by listing out steps?.

Also I have worked out A^-1 but am stuck on solving the system of equations. As I though that you have to work out the inverse of a matrix when doing it for equations (AX=B format). although when I work out A ((2,-1)(3,2)(5,3) it is a 3x2 matrix therefore I am unable to get an inverse. Although the numbers are the same as the A^-1 question but just missing 0's therefore I think it may be something to do with that. Could someone help me please.

Thanks
Prab
 

Attachments

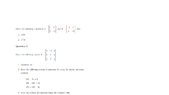
  • Untitled.png
    Untitled.png
    12.2 KB · Views: 52
Physics news on Phys.org
  • #2
Hi I think I may have solved the equations (entering 0s where p1 p2 or p3 do not exist in the equation)

Could someone please still help to see if I have done it correct.
 
  • #3
khehrap said:
I have worked out A^2B but am a bit puzzled on the meaning of A^TB.
$A^T$ denotes the transpose of $A$.

khehrap said:
Hi I think I may have solved the equations (entering 0s where p1 p2 or p3 do not exist in the equation)
Yes, in problem 2, the matrix of the system of equations is $A$.

khehrap said:
Could someone please still help to see if I have done it correct.
Please post your results so that we can check.
 
  • #4
Evgeny.Makarov said:
$A^T$ denotes the transpose of $A$.

Yes, in problem 2, the matrix of the system of equations is $A$.

Please post your results so that we can check.

Hi Evgeny
I ralised that filling in the 0's gives me a matrix that I can use. Although I had already worked out the A^-1 in the first part of the question. therefore working row by row as normal.
The only problem I am facing (must be a calculation error - been doing this assignment for a while :)) is that when I try to work out p2 using matrix inversion shown below:

[1.250 x 2] + [0.375 x 16] + [-0.500 x 21] I am getting -4 not +4. Whereas the answer is +4 (calculation works correctly for both p1 and p3 giving me 3 and 2 respectively.)

I am using the figures above as a-1 gives the figures stated.

I have answered the cramers part too and been given the results 3 4 and 2 for p1 p2 p3.

Thanks
 
  • #5
khehrap said:
[1.250 x 2] + [0.375 x 16] + [-0.500 x 21] I am getting -4 not +4.
The middle number in $A^{-1}$ is $6/8=0.75$, not 0.375. See WolframAlpha.
 

FAQ: Some help on a matrix question please.

What is a matrix question?

A matrix question is a type of survey question that presents a grid or table of options for respondents to choose from. It is commonly used to gather data on a variety of topics, such as preferences, attitudes, and demographics.

How do I create a matrix question?

To create a matrix question, you will need to determine the topic you want to gather information on, choose the appropriate question type (e.g. multiple choice, Likert scale), and create a grid or table with corresponding answer options for each row and column.

What are the advantages of using a matrix question?

The main advantage of using a matrix question is that it allows for a more organized and efficient collection of data. It also allows for more complex and nuanced responses, as it offers multiple answer options for each question.

How do I analyze the data from a matrix question?

To analyze the data from a matrix question, you can use statistical software or tools to generate charts, graphs, and tables. You can also calculate the mean, median, and mode of responses to identify patterns and trends.

Are there any drawbacks to using a matrix question?

One potential drawback of using a matrix question is that it can be time-consuming for respondents to answer, especially if the grid or table is large. It can also be challenging for researchers to analyze the data if there are a large number of response options.

Similar threads

A Trace of the inverse of matrix products
Replies
2
Views
2K
A Similarity transformation changing the determinant to 1
Replies
20
Views
2K
I Eigenproblem for non-normal matrix
Replies
5
Views
2K
A What Is the Significance of the Matrix Identity Involving \( S^{-1}_{ij} \)?
Replies
3
Views
1K
I Meaning of Third Eigenvalue in a Tilted Ellipse in a 3x3 Matrix
Replies
3
Views
2K
I Rotate Functions with Derivatives: A Quantum Mechanics Homework
Replies
2
Views
2K
MHB Showing that a matrix is a homomorphism
Replies
2
Views
2K
MHB Finding Matrix D Without Calculating P Inverse: Help Appreciated!
Replies
2
Views
1K
I A regular matrix <=> mA isomorphism
Replies
11
Views
2K
I Proof concerning the Four Fundamental Spaces
Replies
14
Views
2K

Hot Threads

Recent Insights

Back
Top