Rotate Functions with Derivatives: A Quantum Mechanics Homework

[Oliver321]

TL;DR

How is it possible to rotate a function (for example the 3D wave function) by an infinitesimal angle by using derivatives?

I was solving a problem for my quantum mechanics homework, and was therefore browsing in the internet for further information. Then I stumbled upon this here:

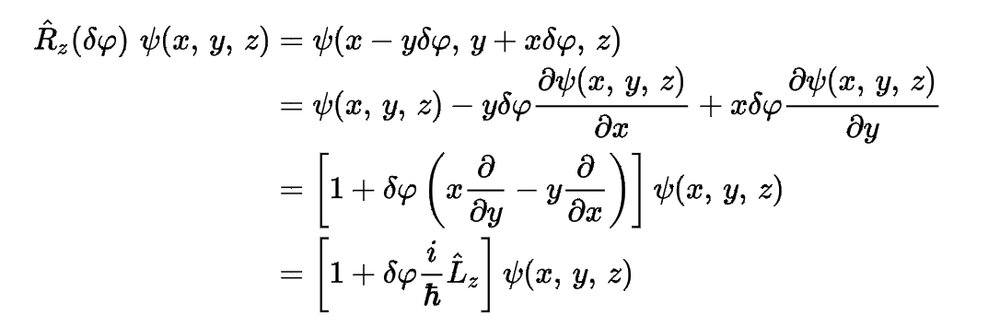
R is the rotation operator, δφ an infinitesimal angle and Ψ is the wave function.
I know that it is able to rotate a curve, vector... with a rotation matrix. But how is it possible to rotate a function only with derivatives? I tried to rephrase a function f(x) as a curve, applying the 2D rotation matrix and small angle approximation and convert it back to an explicit function f(x). But I did not get the same answer.
My question is now: how does this work and what’s the connection to the rotation matrix?

I am really thankful for every help!

 

[DrClaude]

Momentum is the generator of translation, so you can picture infinitesimal translations in x and y as a rotation in the xy plane.

Note that the equation you get is only for infinitesimal rotations, and that the rotation operator around the z axis becomes $e^{- i \hat{L}_z \varphi / \hbar}$ for finite rotations, see
https://en.wikipedia.org/wiki/Rotation_operator_(quantum_mechanics)

 

[jk22]

I was around the same problem but outside of course material is this correct ?

Suppose $\psi\in C^\infty(\mathbb{R}^3,\mathbb{C})$ then the rotation of coordinates should correspond to a phase : $e^{i\phi}\psi(\vec{x})=\psi(R\vec{x})\Rightarrow \phi=i(log(\psi(\vec{x})-log(\psi(R\vec{x})))$ ?

I asked myself : What about if $\psi(\vec{x})\in \mathbb{C}^2$ ?