Something I don't understand about a simple tension problem

[student34]

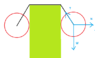
Imagine a tall block of wood sitting on the ground. Then imagine a rope resting on the block with both ends dangling off both sides of the block. Then someone attaches a ball to both ends of the rope. Assume the balls are equal in mass, thus the system is in equilibrium. Now the middle of the rope is still resting on the top of the block, but the ends are now spanned out, say 45 degrees, along the sides of the block because of the radius of the balls attached to the ends of the rope that are hanging off the sides of the block, but not touching the ground. Also assume no friction anywhere.

To my amazement, my textbook has the tension force of the rope being greater than the force of gravity (the only applied force that I can find). The textbook implies a horizontal force x in addition to the vertical force of gravity y. Tension becomes (x^2 + y^2)^(1/2).

I have my first-year university physics and probably should know where the horizontal force is coming from, but I don't.

If "God" shut off the gravity, then there would be no tension, so how is the vertical force of gravity causing more force perpendicular to its vertical vector, which ultimately creates a larger force in the tension?

 

[Merlin3189]

Interesting question.
Have you drawn a diagram?
Then mark on the forces on the balls.

 

[student34]

I assume that there is a normal force x acting on the ball from the wall horizontally. And of course there is a positive vertical -y force reacting to the negative gravitational force y. For the life of me I cannot make sense of where this normal force is coming from (granted I know it is the virtual force particles repelling each others' surfaces because of the electrons). But how did the normal force arise as an applied force and not just a component of gravity (like when the common still block questions with blocks that are held in place on a ramp with friction; in that case the normal force is really just a component of gravity and not a force that creates a greater vector force than the gravity). Somehow gravity alone causes a greater force than itself (at 45 degrees in this example) in this problem.

 

[Merlin3189]

Just draw the diagram! Then it is obvious where the forces come from.

The string is pulling the ball towards the wall. The wall resists and pushes back.

The normal force is not a component of gravity: they are orthogonal.

Edit: The tension is greater than gravity, because the tension is providing opposition to two forces on the ball: the vertical force of gravity on the ball and the horizontal force of the block on the ball.

 

[CWatters]

This problem is similar to the washing line or tightrope problem. Its not possible to tighten the rope to make it perfectly straight. To do so the tension has to be infinite.

 

[student34]

Just draw the diagram! Then it is obvious where the forces come from.
View attachment 232547
The string is pulling the ball towards the wall. The wall resists and pushes back.

The normal force is not a component of gravity: they are orthogonal.

Edit: The tension is greater than gravity, because the tension is providing opposition to two forces on the ball: the vertical force of gravity on the ball and the horizontal force of the block on the ball.

I knew the diagram for this. My issue is that the normal force seems to come from nowhere. The only applied force that I can identify is gravity. Where did the force that is causing the normal force come from?

 

[student34]

This problem is similar to the washing line or tightrope problem. Its not possible to tighten the rope to make it perfectly straight. To do so the tension has to be infinite.

I am not arguing against the answer. My concern is how does Fg go from a vertical force to a vertical force and a horizontal force which is a force vector greater than Fg? It is not making sense at all.

 

[Merlin3189]

The string is not vertical. Therefore it is pulling the ball towards the block. If you cut the string, the normal force will reduce to zero.
The normal force is a reaction to the force of the ball on the block

 

[student34]

The string is not vertical. Therefore it is pulling the ball towards the block. If you cut the string, the normal force will reduce to zero.
The normal force is a reaction to the force of the ball on the block

But what causes the normal force? [edit] We know that gravity causes Fg, the vertical component.

 

[Merlin3189]

The normal force of the block on the ball is a reaction to the normal force of the ball on the block.
The ball is being pulled to the side by the tension in the string. It "tries" to move to the side, but the block is in the way. The ball pushes the block. The block pushes back.

Why is there tension in the string? Because gravity is pulling the ball down and the string is pulling it up.
IF the string could pull vertically on the ball, we'd all be happy and the tension would equal the weight. But it can't. It's pulling at an angle (45^o). That is inefficient (in a non-physics sense) and it has to pull harder than it would if it were vertical. That's why the tension is greater than the weight. As a previous person said, if the angle were even less vertical, the string would have to pull even harder and if the string became horizontal, it would have to pull infinitely hard (ie. it couldn't stop it falling a bit)

If there's a lot of tension in the string, the weight can only counter part of it. The rest, the horizontal component, can not be countered by the vertical gravitational force. That is countered by the block. IF you just did the sums, you would find that whatever the tension in the string (as the position of the ball is varied) the vertical component of that force is always EXACTLY equal to the weight. It is the horizontal component which varies. <Edit:> with the angle of pull.

The sizes of the forces are all consistent. Just work them out.
Since the ball does not move, no work is done by any of the forces. There is a conservation of energy principle, but there is no conservation of force principle. A 10 N force is not limited to be a 10 N force for ever. Use a lever or a pulley and it can become a 100 N force. No problem. That's what you have here, an arrangement of objects which multiplies the force.

 

[CWatters]

Force isn't "conserved" so its not "strange" that a small force can create a larger one. Do you understand levers, wedges, gears, ropes & pulleys? They can all produce forces larger than the applied force and in a different direction. There isn't really anything surprising going on, just Newtons laws and geometry.

 

[student34]

The normal force of the block on the ball is a reaction to the normal force of the ball on the block.
The ball is being pulled to the side by the tension in the string. It "tries" to move to the side, but the block is in the way. The ball pushes the block. The block pushes back.

Why is there tension in the string? Because gravity is pulling the ball down and the string is pulling it up.
IF the string could pull vertically on the ball, we'd all be happy and the tension would equal the weight. But it can't. It's pulling at an angle (45^o). That is inefficient (in a non-physics sense) and it has to pull harder than it would if it were vertical. That's why the tension is greater than the weight. As a previous person said, if the angle were even less vertical, the string would have to pull even harder and if the string became horizontal, it would have to pull infinitely hard (ie. it couldn't stop it falling a bit)

If there's a lot of tension in the string, the weight can only counter part of it. The rest, the horizontal component, can not be countered by the vertical gravitational force. That is countered by the block. IF you just did the sums, you would find that whatever the tension in the string (as the position of the ball is varied) the vertical component of that force is always EXACTLY equal to the weight. It is the horizontal component which varies. <Edit:> with the angle of pull.

The sizes of the forces are all consistent. Just work them out.
Since the ball does not move, no work is done by any of the forces. There is a conservation of energy principle, but there is no conservation of force principle. A 10 N force is not limited to be a 10 N force for ever. Use a lever or a pulley and it can become a 100 N force. No problem. That's what you have here, an arrangement of objects which multiplies the force.

Thanks, it is helping me to think of other examples where the applied force becomes multiplied, like with pulleys and levers. Torque seems to be what's causing the force to be multiplied. I only got my first-year of physics in university, so I do not know how to "follow" the force to the point where it multiplies, even though we covered torque. My specialty is chemistry and I thought knowing molecular forces would help me, but I seem to keep running into the same problem of "finding" the exact "multiplying cause" for lack of a better term.

 

[student34]

Force isn't "conserved" so its not "strange" that a small force can create a larger one. Do you understand levers, wedges, gears, ropes & pulleys? They can all produce forces larger than the applied force and in a different direction. There isn't really anything surprising going on, just Newtons laws and geometry.

I am thinking about levers, like you mentioned, and how simple torque formulas show how force is in fact multiplied, but I am having trouble understanding how that works. There is something really nonintuitive going on here for me, or at least an aspect of the nature of force that I am forgetting. Like what makes it different that conserved entities?