- #1
ChiralSuperfields
- 1,206
- 132
- Homework Statement
- I am trying to find the speed of sound given that gradient of resonant length of the tube (for the fundamental) vs tuning fork wavelength
- Relevant Equations
- Theoretically ##L_{res}= λ/4##
However, for the graph ##L_{res} =0.2381λ##
The graph is,
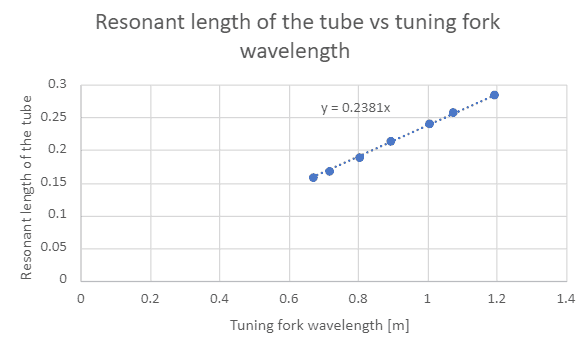
I do not understand why how it is possible to find the speed of sound from the gradient for this graph. Can someone please help?
Many thanks!
I do not understand why how it is possible to find the speed of sound from the gradient for this graph. Can someone please help?
Many thanks!