Sphere and electric field of infinite plate

[annamal]

Homework Statement

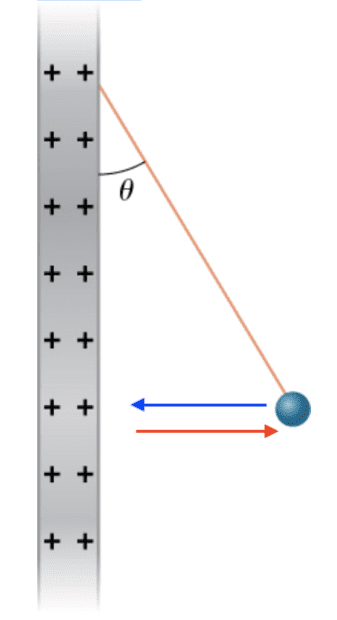
Shown below is a small sphere of mass 0.25 g that carries a charge of $9*10^{-10}$. The sphere is attached to one end of a very thin silk string 5.0 cm long. The other end of the string is attached to a large vertical conducting plate that has a charge density of $30*10^{-6}$. What is the angle that the string makes with the vertical?

Relevant Equations

$\vec E = \frac{\sigma}{2\epsilon}$

The solution says that the tension in the string in the negative x direction is balanced by the force of the plate on the ball (red). Why is the repulsive force of the ball on the plate (in blue) not included in this calculation?

 

[andrewkirk]

The problem requires us to find a position of the ball where the net sum of forces on it from plate, gravity and string is zero, so that the ball remains stationary. We call this a problem in 'statics', as opposed to a problem in 'kinetics' or 'dynamics' that involves motion.
To solve the problem we need only consider forces exerted on the ball, not forces that the ball exerts on other things.

 

[annamal]

The problem requires us to find a position of the ball where the net sum of forces on it from plate, gravity and string is zero, so that the ball remains stationary. We call this a problem in 'statics', as opposed to a problem in 'kinetics' or 'dynamics' that involves motion.
To solve the problem we need only consider forces exerted on the ball, not forces that the ball exerts on other things.

Would the force the ball exerts on the plate equal the force the plate exerts on the ball: $q* \frac{\sigma}{2\epsilon}$?

 

[haruspex]

Would the force the ball exerts on the plate equal the force the plate exerts on the ball: $q* \frac{\sigma}{2\epsilon}$?

What did Newton say?

 

[annamal]

What did Newton say?

Equal and opposite, so I am guessing yes. So on the system of just the plate and the ball, there should be no net force since the electrical forces are equal and opposite?

 

[haruspex]

Equal and opposite, so I am guessing yes. So on the system of just the plate and the ball, there should be no net force since the electrical forces are equal and opposite?

Yes.

 

[annamal]

Is this problem assuming the conducting plate is fixed? Because if it isn't, wouldn't it fly to the left due to the force from the ball?

 

[Delta2]

Is this problem assuming the conducting plate is fixed? Because if it isn't, wouldn't it fly to the left due to the force from the ball?

Yes. For me at least this is self implied, it is like doing a mechanics problem that involves (normal) forces from the ground and asking if the ground is fixed.

 

[haruspex]

Is this problem assuming the conducting plate is fixed? Because if it isn't, wouldn't it fly to the left due to the force from the ball?

No, because just as the horizontal forces balance on the ball they also balance on the plate. But of course some torque must stop the plate/ball system falling over.

 

[annamal]

No, because just as the horizontal forces balance on the ball they also balance on the plate. But of course some torque must stop the plate/ball system falling over.

What are the horizontal forces that balance the plate? There is the force the ball exerts on the plate. There is no mention of a force countering that.

 

[Delta2]

What are the horizontal forces that balance the plate? There is the force the ball exerts on the plate. There is no mention of a force countering that.

I think it must be a component of the force from the string to the plate.

 

[annamal]

I think it must be a component of the force from the string to the plate.

I thought that only holds the ball in place.

 

[haruspex]

I thought that only holds the ball in place.

The string is under tension, so it pulls on whatever it is attached to at its two ends equally.

 

[kuruman]

To @annamal : Could you provide units for the charge on the sphere and the charge density?

I also have a question of interpretation. We have here a conducting plate "that has a charge density of $30*10^-6$. Missing units notwithstanding, when the charged sphere is not in position, the charges can be assumed to be equally distributed on the left and right surfaces as shown in the figure. Is the number given the surface charge density on one of the surfaces or on each of the surfaces?

 

[annamal]

To @annamal : Could you provide units for the charge on the sphere and the charge density?

I also have a question of interpretation. We have here a conducting plate "that has a charge density of $30*10^-6$. Missing units notwithstanding, when the charged sphere is not in position, the charges can be assumed to be equally distributed on the left and right surfaces as shown in the figure. Is the number given the surface charge density on one of the surfaces or on each of the surfaces?

They are SI units so $C/m^2$...although the units are irrelevant to my actual question