- #1
Saitama
- 4,243
- 93
Homework Statement
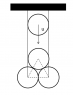
Two equal spheres of mass m are suspended by vertical strings so that they are in contact with their centres at the same level. A third equal sphere of mass m falls vertically and strikes elastically the other two simultaneously so that their centres at the instant of impact form an equilateral triangle in a vertical plane. If u is the velocity of m just before impact, find the velocities just after impact and the impulse of tension of the strings.
Homework Equations
The Attempt at a Solution
After collision, the hanging spheres will gain velocity along the direction of common normal of spheres. (Common normal is the line joining the centres of sphere)
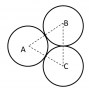
See attachment 2 (I haven't shown the strings and rotated the figure).
Conserving momentum in x-direction,
##mu=mv'+2mv''\cos(\pi/6)##
From the equation of coefficient of restitution,
$$e=\frac{\text{Relative speed after collision}}{\text{Relative speed after collision}}$$
The relative speed before collision is ##u\cos(\pi/6)## and after collision is ##v''-v'\cos(\pi/6)## and for elastic collision, coefficient of restitution is 1. Plugging and rearranging,
$$v''-v'\cos(\pi/6)=u\cos(\pi/6)$$
Solving the two equations I have doesn't give me the right answer. :(
Any help is appreciated. Thanks!