Yroyathon
- 42
- 0
hi again. i totally rocked my physics homework this week, except for this last one.
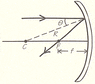
Consider a spherical mirror without making the paraxial approximation (Fig. 36-47, attached as a file). When a ray parallel to the axis makes an angle θ with the radius R at the point of contact, then f, the distance at which the ray crosses the axis, is given by the following.
f = R* (1 - (1 / (2*cosθ)))
Calculate the spread in values of f for a spherical mirror of radius 0.15 m and arc length 45 cm.
Shortest focal length ? cm
Longest focal length ? cm
maybe s=r*θ
i'm not totally clear on what's going on in this problem. i thought it's just a bunch of parallel rays going right and bouncing off the mirror and creating lots of different focal points. and then we just want the biggest and smallest.
so for θ, i figured that the angle between the radius (which I converted to cm) and the base line is also equal to θ. is this right?
then i used s=r * θ , and got θ = 3 radians for this particular radius and arclen. so I figured i should consider values of θ between -3/2 and 3/2, that is, so that the range is 3 radians long and split evenly between positive and negative.
plugging these values into the equation for f, i thought I was just supposed to look for the biggest and smallest values of f. but this didn't get me right answers, so... can't be that simple.
any tips for what to try next? or just conceptual help if my interpretation isn't right?
Thanks a lot.
,Yroyathon
Homework Statement
Consider a spherical mirror without making the paraxial approximation (Fig. 36-47, attached as a file). When a ray parallel to the axis makes an angle θ with the radius R at the point of contact, then f, the distance at which the ray crosses the axis, is given by the following.
f = R* (1 - (1 / (2*cosθ)))
Calculate the spread in values of f for a spherical mirror of radius 0.15 m and arc length 45 cm.
Shortest focal length ? cm
Longest focal length ? cm
Homework Equations
maybe s=r*θ
The Attempt at a Solution
i'm not totally clear on what's going on in this problem. i thought it's just a bunch of parallel rays going right and bouncing off the mirror and creating lots of different focal points. and then we just want the biggest and smallest.
so for θ, i figured that the angle between the radius (which I converted to cm) and the base line is also equal to θ. is this right?
then i used s=r * θ , and got θ = 3 radians for this particular radius and arclen. so I figured i should consider values of θ between -3/2 and 3/2, that is, so that the range is 3 radians long and split evenly between positive and negative.
plugging these values into the equation for f, i thought I was just supposed to look for the biggest and smallest values of f. but this didn't get me right answers, so... can't be that simple.
any tips for what to try next? or just conceptual help if my interpretation isn't right?
Thanks a lot.
,Yroyathon