ag123
- 32
- 5
i'm simulating a small dc motor that is driven by volt = 1.54v, current = 250 milli amps, so that gives me 0.385 watts supplied to the motor
next i attached a 4mm thick circular acrylic disc as a flywheel. so in this simulation i spin up the acrylic disc as a flywheel
my acrylic disc is 12cm (4.7") diameter.
acrylic density 1.18 g/cm cube
https://www.engineeringtoolbox.com/density-solids-d_1265.html
next i get the relevant equations:
https://en.wikipedia.org/wiki/Flywheel
E = 1/2 . I . w^2 ... (1)
I ~ moment of internia
w ~ angular velocity
https://en.wikipedia.org/wiki/Torque
power = torque . w ... (2)
then from (1):
E / t = 1/2 . I . w^2 / t
power = 1/2 . I . w^2 / t ... (3)
w = sqrt ( 2 . power . t / I )
now i assume power is that coming from the motor which is 'constant'
so in this way i can plot the angular velocity over time
next subst (3) into (2):
1/2 . I . w^2 / t = torque . w
torque = 1/2 . I . w / t
so in this way i can plot the torque over time
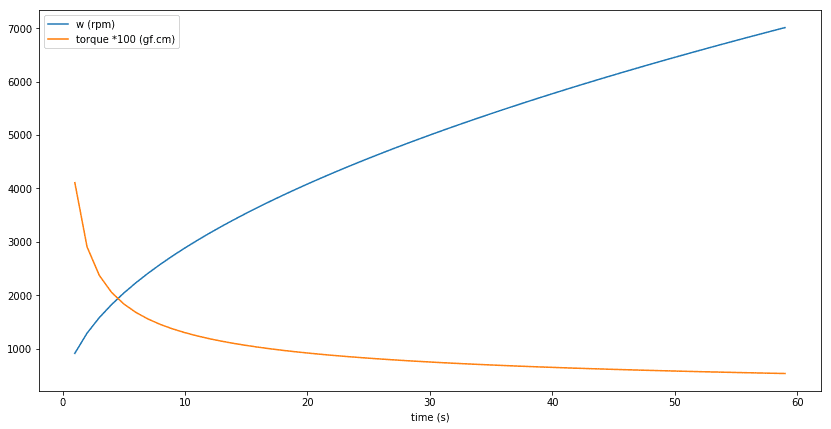
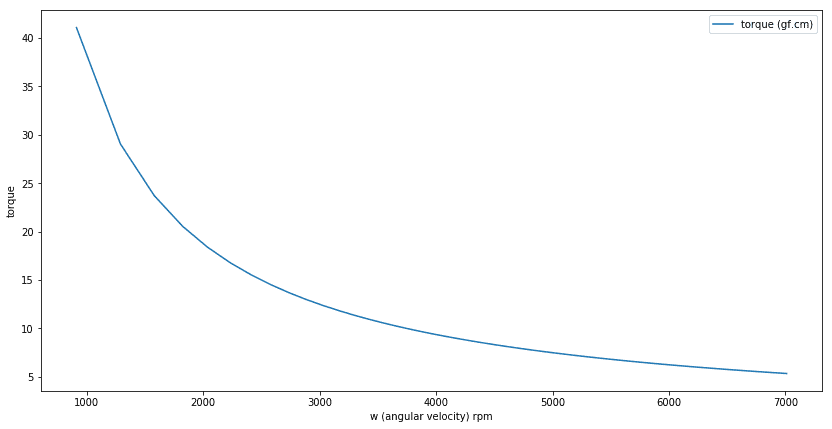
the results look 'surprising', apparently the torque falls even as the acrylic disc / flywheel is spun up (this still seemed quite 'ok')
next the angular velocity i converted it to rpm (revolution per minute) increases but is not linear
what is a little astonishing is the disc spinning at 7000 rpm after 60 secs for a 12cm (4.7") x 4mm thick acrylic disc
that motor delivers a minuscule 0.385 watts !
any mistakes in these calcs?
next i attached a 4mm thick circular acrylic disc as a flywheel. so in this simulation i spin up the acrylic disc as a flywheel
my acrylic disc is 12cm (4.7") diameter.
acrylic density 1.18 g/cm cube
https://www.engineeringtoolbox.com/density-solids-d_1265.html
next i get the relevant equations:
https://en.wikipedia.org/wiki/Flywheel
E = 1/2 . I . w^2 ... (1)
I ~ moment of internia
w ~ angular velocity
https://en.wikipedia.org/wiki/Torque
power = torque . w ... (2)
then from (1):
E / t = 1/2 . I . w^2 / t
power = 1/2 . I . w^2 / t ... (3)
w = sqrt ( 2 . power . t / I )
now i assume power is that coming from the motor which is 'constant'
so in this way i can plot the angular velocity over time
next subst (3) into (2):
1/2 . I . w^2 / t = torque . w
torque = 1/2 . I . w / t
so in this way i can plot the torque over time
the results look 'surprising', apparently the torque falls even as the acrylic disc / flywheel is spun up (this still seemed quite 'ok')
next the angular velocity i converted it to rpm (revolution per minute) increases but is not linear
what is a little astonishing is the disc spinning at 7000 rpm after 60 secs for a 12cm (4.7") x 4mm thick acrylic disc
that motor delivers a minuscule 0.385 watts !
any mistakes in these calcs?
Last edited: