Spring attached to string on one side, mass on the other.

[mrdoe]

This is a problem I came up with myself, so it's not homework and so I didn't post in that forum.

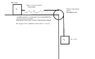
Suppose a mass m1 rests on a frictionless table. m1 is directly connected to a massless ideal spring at equilibrium length of spring constant k which is connected to a string going over a pulley of mass m3 and radius r (and rot. inertia 0.5m3r^2), which is connected after the pulley to a mass m2.

Determine the equation for the motion of mass m1 when m2 is released. (dig. attached).

How would you go about doing this problem? I can't seem to get started because I can't figure out how to find the length the spring will initially be extended.

relevant equations:
F = -kx
Conservation of energy, probably.
All the angular/linear kinematics equations.

edit:sorry reread the rules just then, mods please move this to the homework forum (i thought the restriction didn't apply to independent study)

 

[tiny-tim]

Hi mrdoe!

This is a problem I came up with myself …
…
Determine the equation for the motion of mass m1 when m2 is released. (dig. attached).

How would you go about doing this problem? I can't seem to get started because I can't figure out how to find the length the spring will initially be extended.

Use conservation of energy.

And since you came up with this problem yourself, I'm surprised you've forgotten that you decided that "The spring is held at equilibrium before mass 2 is released" (in the diagram) … which I assume means that the spring is held at its natural length.

 

[jack action]

Since it is a frictionless table, the spring will never deform.

Imagine the problem another way: hold m1 over m2 in the air (no pulley), linked by the same string and spring. release them both under acceleration g. What happen? Both fall at the same velocity and the spring never get stretched, because there are no opposite forces.

You need friction to stretch the spring. And, in that case, the equation of motion would be easy since m2 would move while m1 is at rest. m1 will start to move when the spring force will overcome the static friction. At this point, motion of m1 will be the same as motion m2 with the extra distance created by the stretched spring.

 

[mrdoe]

Thanks, it makes sense now.
Intuitively the initial tug of gravity on mass m2 would stretch the spring and move m1 at the same time, but I guess we live in a world full of friction so that isn't really accurate.