Totalderiv
- 69
- 1
Hey I'm currently a freshman math major and just registered for my spring classes. When I went to my adviser, she thought I was insane for taking three math classes at one time. Am I insane?
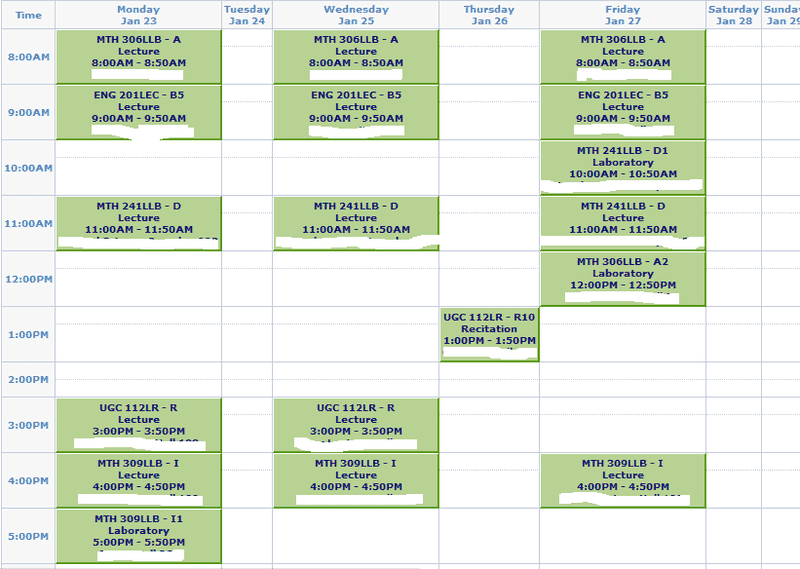
Schedule:
-College Calculus 3
-Introduction to Differential Equations
-Introduction to Linear Algebra
-World Civilization 2
-May take Advanced Writing 1 as well
Schedule:
-College Calculus 3
-Introduction to Differential Equations
-Introduction to Linear Algebra
-World Civilization 2
-May take Advanced Writing 1 as well
Last edited:
