Spring force after fixating with limited stiffness

[rmwanders]

Hi folks,

I have an interesting problem here from the real world, it's a design i am working on.

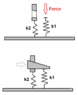
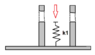
So I have an object that is pressed by an hydraulic press with 50kN, let's call it F_before. Then I drive in a jig to fixate it. But the part that holds the jig has a limited stiffness. Hence if I release the hydraulic press the system will bounce up and the force in the system will be less than 50 kN, but how much?

The way I see it the springs are in series and I can use the conservation of spring energy to find the ratio between F_after and F_before.
F_after/F_before = sqrt(k2/(k1+k2))

Is this correct? The square root in the solution looks kinda odd to me.

 

[Dale]

Does the jig prevent rotation? Is the jig considered very stiff or do we need to consider deformations of the jig itself?

 

[rmwanders]

Hi, yes the jig prevents rotation and is considered very stiff.

In reality the spring k2 is a bus with limited stiffness that goes around k1. The jig goes through the bus supporting against the inner spring on the left and the right sides. see picture
I think the jig and any deformations in it can be considered part of spring k2 once I transfer my conceptual design to a finite element program.

But for now I am trying to get a more basic understanding of my design.

 

[Dale]

Hi, yes the jig prevents rotation and is considered very stiff.

So then you can consider the springs to act as one joint spring. The stiffness of the joint spring is just $k_{joint}=k_1+k_2$

 

[Lnewqban]

As I see it, after the press action is removed, spring 1 will be under compression load, which will be equal to the tension load of spring 2.
Is that statement correct?

 

[rmwanders]

Yes indeed. Because the springs are in series. But the question is how much remains of the tension/compression force after the jig is placed and the press is released. It should be less that the 50 kN the press applied

 

[A.T.]

F_after/F_before = sqrt(k2/(k1+k2))

Is this correct? The square root in the solution looks kinda odd to me.

I also don't think the root should be there.

Consider the force over jig displacement (relative to the release position) graphs of the two springs:

spring_1: intercept = F_before, slope = -k1
spring_2: intercept = 0, slope = k2

F_after is where they intersect after some jig displacement d:

(F_before - F_after) / d = k1
F_after / d = k2

Solving for F_after leads to:

F_after = F_before * k2/(k1+k2)

 

[hutchphd]

I agree with @A.T.

And to be pedantic (it is what we do! ) the energy in the springs is not conserved

Summary:: spring force after fixating with limited stiffness

The way I see it the springs are in series and I can use the conservation of spring energy to find the ratio between F_after and F_before.

This is because you do negative work on them during the relaxation. If you didn't, they would oscillate (until "friction" dissipated the energy).

 

[A.T.]

And to be pedantic (it is what we do! ) the energy in the springs is not conserved

Yes, the springs change because they tend towards a lower potential energy state.

In particular, the force on the jig by spring_2 is not equal to the force by spring_1, while the displacement is the same for both. So the positive work by the jig on spring_2 is smaller than the negative work on spring_1. The jig would gain kinetic energy, which you either remove during the process or it dissipates in osculations.

 

[rmwanders]

Thanks a lot guys! It all makes sense now :)