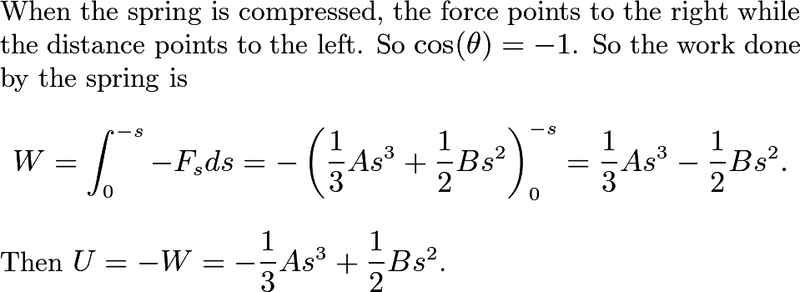The discussion focuses on the relationship between spring force and displacement, emphasizing the need to correctly integrate work done by a spring. The equation for work done is clarified as (1/3)As^3 + (1/2)Bs^2, highlighting that the external force compresses the spring. Participants note that the integration bounds should be from 0 to s, as s represents the displacement from equilibrium, not a specific position. The conversation also clarifies that in the standard formula F = kx, x denotes distance rather than position. Understanding these concepts is crucial for accurately calculating work in spring mechanics.