MatinSAR
- 673
- 204
- Homework Statement
- A massless spring with no mass attached to it hangs from the ceiling. Its length is 0.2
meter. A mass m is now hung on the lower end of the spring. Imagine supporting the mass
with your hand so that the spring remains relaxed (that is, not expanded or compressed),
then suddenly remove your supporting hand. The mass and spring oscillate. The lowest
position of the mass during the oscillations is 0.1 m below the place it was resting when
you supported it. What is the spring constant?
- Relevant Equations
- Conservation of energy.
I know that we can answer it using conservation of energy or using N's 2nd law.
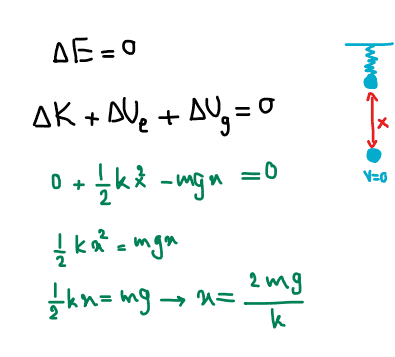
Using N's 2nd Law:
##F = mv \frac {dv}{dx}##
##Fdx = mvdv##
For spring we have : ##F=-kx##
##(mg-kx)dx=mvdv##
We'll get same result using above equation.
My question:
Average spring force from 0 to x is ##-\frac {1}{2}kx## ... Can't we say that at lowest point spring force could be equal to ##-\frac {1}{2}kx## instead of ##-kx##? Then at lowest point we have ##mg = -\frac {1}{2}kx## ...
Using N's 2nd Law:
##F = mv \frac {dv}{dx}##
##Fdx = mvdv##
For spring we have : ##F=-kx##
##(mg-kx)dx=mvdv##
We'll get same result using above equation.
My question:
Average spring force from 0 to x is ##-\frac {1}{2}kx## ... Can't we say that at lowest point spring force could be equal to ##-\frac {1}{2}kx## instead of ##-kx##? Then at lowest point we have ##mg = -\frac {1}{2}kx## ...