Springs and dampers in series and parallell

[MannyPacquiao]

Homework Statement

Ok here it goes, we all know that 2 springs in series (k1, k2) can be expressed as one spring with spring constant k using the following equation.
<br /> k=\frac{1}{\frac{1}{k_{1}}+\frac{1}{k_{2}}}<br />
The same holds for 2 dampers c1 and c2.
<br /> c=\frac{1}{\frac{1}{c_{1}}+\frac{1}{c_{2}}}<br />

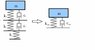
But what would happen if we have the system shown in the attached file. Point X is connected to S via a spring k1 and damper c1 in parallell, and point S is conncted to W via a spring k2 and damper c2 in parallell.

My question: If I'm only interested in points X and W, can the system be simplified into a one spring and one damper system?

Homework Equations

Already stated

The Attempt at a Solution

My initial guess is that the dynamics between X and W can be expressed with one spring and one damper with contants
<br /> k=\frac{1}{\frac{1}{k_{1}}+\frac{1}{k_{2}}}, c=\frac{1}{\frac{1}{c_{1}}+\frac{1}{c_{2}}}<br />

For this perticular question the masses are irrelevant, however in my original problem X and W have masses but S is massless.

Thanks in advance

 

[DJbijvoet]

Hi MannyPacquiao,

Do you already have the solution and if so can you share it with me. I am also interrested in the answer!


Dirk-Jan.

 

[MannyPacquiao]

Sorry I still don't know

 

[kuza]

Bump.

I've come across the same problem. I'm trying to model almost the same system in Simulink - does anyone know if a series of two damper + spring can be substituted by one damper parallel to one spring, as shown above?

Thanks in advance.

Edit: I'm thinking that two dampers in series have their damping coefficient added, similar to electrical resistance?

 

[testing1234]

Please could anyone confirm that dampers behave the same as springs when they are in series and parallel?

Thanks in advance.

 

[sshzp4]

Please could anyone confirm that dampers behave the same as springs when they are in series and parallel?
Thanks in advance.

dampers behave the same as springs when they are in series and parallel? Yes.

Are such formulas useful? No! Always construct free body diagrams with well-defined inertial/non inertial reference frames.

Look up 'mechanical impedance'. The standard MKC model is useful only because it leads to compact theoretical solutions, so they are good for an initial/undergrad study.

For a better understanding of what's up with springs and dampers in assorted combinations, first brush up on the reference frame concepts on physics. Then consider that force from damping is proportional to the velocity of the end plates of a damper. So, the force is proportional to the relative velocity of one plate with respect to the other.

The analogy with a spring is, the force from spring is proportional to the displacement of one end of the spring relative to the displacement of the other end. So as long as you keep track of your coordinate systems/state space variables with respect to the reference frames, you will get it right.

Even most advanced graduate level vibrations classes don't talk about it (but professionals do know about it). You can't usually derive theoretical solutions for such problems, so it's left for a quick mention, or none, in chapters dealing with numerical modeling/modal analysis.

Regards,

Sid/sshzp4

 

[gneill]

It might be instructive to have a look at:

http://lpsa.swarthmore.edu/Analogs/ElectricalMechanicalAnalogs.html

Particularly the examples towards the end.

 

[J_R]

Hi,

Can anyone help me formulate the equivalent spring and damper coefficients, for the problem represented on picture below.

Can i just use the equations from the first post in this thread (only instead of using two springs in series, i would use three), or would that be wrong?

 

[gneill]

Hi,

Can anyone help me formulate the equivalent spring and damper coefficients, for the problem represented on picture below.

Can i just use the equations from the first post in this thread (only instead of using two springs in series, i would use three), or would that be wrong?

I don't believe that an accurate equivalent consisting of one spring and one damper can be made. Consider that in your diagram the spring k1 is not damped at all. If set in motion it would oscillate indefinitely (presuming it has some mass or a mass attached to it). Your suggested equivalent has the whole spring damped, so it cannot achieve that behavior.

 

[J_R]

Thank you Mentor for your reply. It looks like I will have to define d1 as well.