Square pivoted at corner-conservation of energy

[natasha13100]

Homework Statement

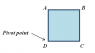
A uniform square plate ABCD has mass 2.5 kg and side length 0.8 m. The square is pivoted at vertex D and initially held at rest so that sides AB and CD are horizontal (see the diagram). After it is released, the plate swings downward, rotating about the pivot point. Resistive force can be neglected. The acceleration due to gravity is g = 9.8 m/s². The rotational inertia of a square plate of side d relative to the axis perpendicular to the plate and passing through the center of mass is md²/6. Find (a) the rotational inertia about the pivot, (b) the angular speed ω of the square at the moment when BD is horizontal, (c) the linear speed v of B at the moment when BD is horizontal, and (d) the linear speed of B at the moment when B is straight down

Homework Equations

I_cm=md²/6
I_p=I_cm+mx^2 where x=distance from pivot to cm
conservation of energy (in this case U_grav,i=K_trans+K_rot+U_grav,f)
v=ωr

The Attempt at a Solution

(a) I_cm=2.5*0.8²/6=4/15
x=d√(2)/2=.4√(2)
I_p=4/15+2.5(.4√(2))²=52/15

(b) U_grav=mgh where h=height above pivot
U_grav=mgd/2=9.8
K_trans=1/2mv²=1/2mr²ω² where r=radius(I'm not sure about what to consider the radius, but I would guess it is the distance from the pivot to the center of mass)
K_trans=1/2m(d√(2)/2)²ω²=1/4md²ω²=1/4*2.5*(.32)²ω²=.064ω²
K_rot=1/2*44/75ω²=22/75*ω²
9.8=ω²(.064+22/75)
ω²=9.8/(134/375)=3675/134
ω=5.236924015

(c)v=ωb where b=distance from pivot to B
v=ωd√(2)=5.236924015*0.8√(2)=5.924903173

(d)9.8=ω²(.064+22/75)-mgd√(2)/2
9.8-2.5*0.8√(2)/2=(49-5√(2))/5=ω²(.064+22/75)
ω=√((49-5√(2))/5/(.064+22/75))=4.844345769
v=ωr=d√(2)=ω0.8√(2)=5.480751589

 

[Simon Bridge]

It is a good idea to put your reasoning down so people don't have to guess - it also helps us taylor the replies to the way you think. Don't forget to write down the units in your answers.

(a) the rotational inertia about the pivot,

Parallel axis theorem - which you appear to have done with:

x=d√(2)/2=.4√(2)

... you seem to be saying that the center of mass lies half-way along a diagonal? (i.e. x=|DB|/2)
Another approach would have been to mark the com by the letter O and realize that the triangle DCO is of type 1-1-√2 with CD forming the hypotenuse. By similar triangles: |DC|=d x=|DO|=d/√2

(b) the angular speed ω of the square at the moment when BD is horizontal,

Conservation of energy - the amount the com falls goes to kinetic energy.

U_grav=mgh where h=height above pivot
Ugrav=mgd/2=9.8

... you have defined your zero for potential energy at the pivot height - well done. This appears to be saying that the com falls a distance d/2=0.4m ... is this correct?

Ktrans=1/2mv2=1/2mr2ω2 where r=radius(I'm not sure about what to consider the radius, but I would guess it is the distance from the pivot to the center of mass)

Only if point B is at the center of mass - is it? (i'm guessing this is the bit you want help on.)
Why not just use the rotational kinetic energy: $K_{rot}=\frac{1}{2}I\omega^2$ ... you found I in part (a).

(c) the linear speed v of B at the moment when BD is horizontal, and (d) the linear speed of B at the moment when B is straight down.

Relationship between angular velocity and tangential velocity. It only asks for speed you you don't have to worry about the directions.

 

[natasha13100]

Sorry about not making myself clear enough. I believe if I can figure out part b then I can get the rest on my own. Thanks for the tip about K_rot. All of our formulas are based on center of mass and that was making it more complicated. We are also supposed to be using both rotational and translational kinetic energy
If I understand correctly, U_grav=K_rot,p
mgd/2=1/2I_pω²
ω=√(mgd/I_p)=2.5*9.8*.8*15/52=147/26

 

[Simon Bridge]

You do need to be careful about when you need the translational as well as the rotational stuff.
But you can do everything you need in the reference frame of the pivot point, which makes it easier.

You have understood what I was saying though.
Rinse and repeat :)

Note: you appear to have been clear enough - but if you add a brief description of your thinking to your working, you will make it easier for people to give you full marks ;) It can be as simple as just naming the principle you are using to get that step.