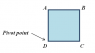
- #1
natasha13100
- 58
- 0
Homework Statement
A uniform square plate ABCD has mass 2.5 kg and side length 0.8 m. The square is pivoted at vertex D and initially held at rest so that sides AB and CD are horizontal (see the diagram). After it is released, the plate swings downward, rotating about the pivot point. Resistive force can be neglected. The acceleration due to gravity is g = 9.8 m/s2. The rotational inertia of a square plate of side d relative to the axis perpendicular to the plate and passing through the center of mass is md2/6. Find (a) the rotational inertia about the pivot, (b) the angular speed ω of the square at the moment when BD is horizontal, (c) the linear speed v of B at the moment when BD is horizontal, and (d) the linear speed of B at the moment when B is straight down
Homework Equations
Icm=md2/6
Ip=Icm+mx^2 where x=distance from pivot to cm
conservation of energy (in this case Ugrav,i=Ktrans+Krot+Ugrav,f)
v=ωr
The Attempt at a Solution
(a) Icm=2.5*0.82/6=4/15
x=d√(2)/2=.4√(2)
Ip=4/15+2.5(.4√(2))2=52/15
(b) Ugrav=mgh where h=height above pivot
Ugrav=mgd/2=9.8
Ktrans=1/2mv2=1/2mr2ω2 where r=radius(I'm not sure about what to consider the radius, but I would guess it is the distance from the pivot to the center of mass)
Ktrans=1/2m(d√(2)/2)2ω2=1/4md2ω2=1/4*2.5*(.32)2ω2=.064ω2
Krot=1/2*44/75ω2=22/75*ω2
9.8=ω2(.064+22/75)
ω2=9.8/(134/375)=3675/134
ω=5.236924015
(c)v=ωb where b=distance from pivot to B
v=ωd√(2)=5.236924015*0.8√(2)=5.924903173
(d)9.8=ω2(.064+22/75)-mgd√(2)/2
9.8-2.5*0.8√(2)/2=(49-5√(2))/5=ω2(.064+22/75)
ω=√((49-5√(2))/5/(.064+22/75))=4.844345769
v=ωr=d√(2)=ω0.8√(2)=5.480751589