bwana
- 82
- 2
- TL;DR
- In the derivation of the SR equation using a 'light clock', the final equation seems to depend on the direction of the photon path relative to the train
One of my first exposures to special relativity was looking at a 'light clock' where a photon is emitted and captured by a detector whilst traveling on a train. The passenger sees the photon go straight up.
 The distance traveled by this photon in a given time, t, is c t
The distance traveled by this photon in a given time, t, is c t
An observer however sees the photon traveling diagonally as the train moves.
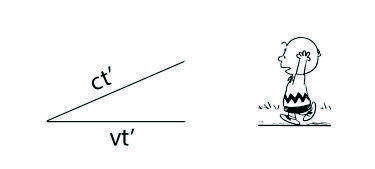
The observer then connects the the two frames of reference with a triangle.
 And this allows the derivation of the equation.
And this allows the derivation of the equation.
However, on a different train, the passenger sets up the light clock differently.

And the observer sees things somewhat differently.
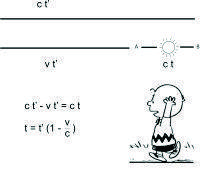 And so he gets a different equation.Yet a third passenger sets things up differently again.
And so he gets a different equation.Yet a third passenger sets things up differently again.

And now the observer sees something yet different and is totally thrown for a loop
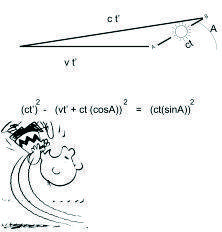
It's SOOO CONFUSING!

Please make it stop!
We are still dealing with inertial frames so which is the 'correct' model? Obviously, the first depiction is always portrayed so there must be an explanation supporting its validity over the others.
An observer however sees the photon traveling diagonally as the train moves.
The observer then connects the the two frames of reference with a triangle.
However, on a different train, the passenger sets up the light clock differently.
And the observer sees things somewhat differently.
And now the observer sees something yet different and is totally thrown for a loop
It's SOOO CONFUSING!
Please make it stop!
We are still dealing with inertial frames so which is the 'correct' model? Obviously, the first depiction is always portrayed so there must be an explanation supporting its validity over the others.