Calculating the Second Moment of Area for Floating Bodies

[tomtomtom1]

Homework Statement

Stability Of Floating Bodies

Relevant Equations

BM = I / V

Hello all

I was hoping someone could help shed some light on understanding an equation for floating bodies.

I am trying to work out the distance between B and M shown in the sketch below:-

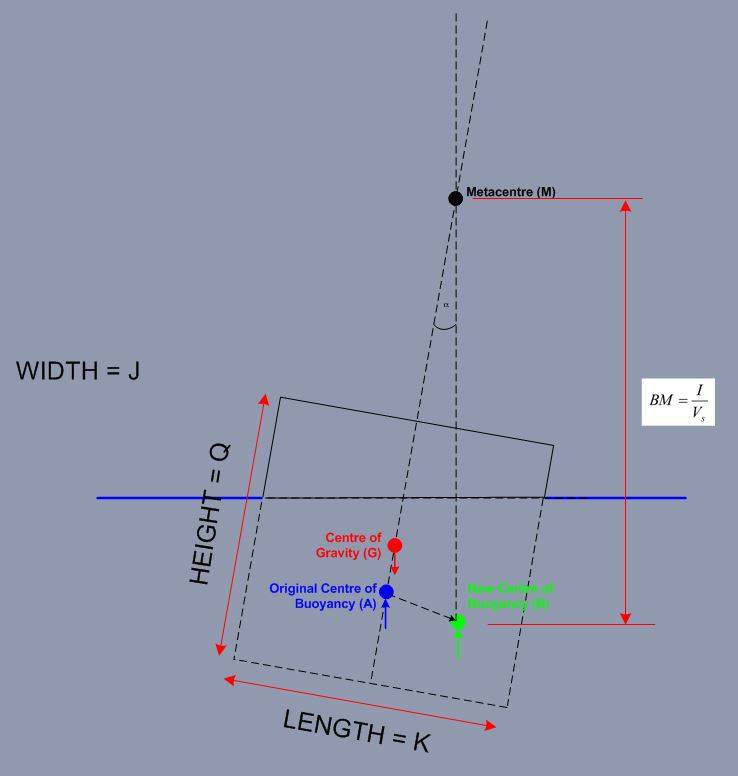
I have been given the equation:-

BM = I/V

BM = is the distance from center of buoyancy to the meta center
I = Is the second moment of area
V = Volume of the submerged portion of the body.

I just want to know how to calculate I?

Is I worked out for the entire floating board or is I worked out for just the portion of the body above the water line or is I calculated to the portion of the body below the water line?

I know that I is bd^3/12 but in my example do i use q for b and k for d - how do you know what values to use and what portion of the bosy I relates to?

Can anyone help?

Thank you.

 

[CptXray]

I remember that there's something about stability of floating bodies in "Physics of Continuous Matter Exotic and Everyday Phenomena in the Macroscopic World" by B. Lautrup. Maybe that will help?

 

[haruspex]

Is I worked out for the entire floating board or is I worked out for just the portion of the body above the water line or is I calculated to the portion of the body below the water line?

It is the second moment of area of the horizontal slice through the hull at the waterline. This slice is also known as the waterplane.
So use k for d, but b will be the length of the hull (assuming it is just a rectangular box).
This length will also feature in the volume, so will cancel out.