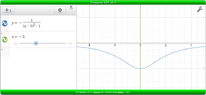
SUMMARY
The range of the reciprocal function g(x) = -1/((x+3)^2 + 1) is determined to be (-1, 0]. The original function f(x) = -(x+3)^2 - 1 has a maximum value of -1, which corresponds to the horizontal asymptote of the reciprocal function. The graph of g(x) is symmetric about the line x = -3 and approaches the x-axis as a horizontal asymptote. The minimum value occurs when the denominator is minimized, confirming the range of g(x).
PREREQUISITES
- Understanding of reciprocal functions
- Knowledge of quadratic functions and their properties
- Familiarity with graphing techniques for rational functions
- Basic concepts of asymptotes in function analysis
NEXT STEPS
- Study the properties of reciprocal functions in detail
- Learn how to identify and graph horizontal and vertical asymptotes
- Explore the implications of function symmetry in graphing
- Investigate the discriminant of quadratic equations and its role in determining ranges
USEFUL FOR
Students and educators in mathematics, particularly those focusing on algebra and function analysis, as well as anyone interested in understanding the behavior of reciprocal functions and their graphs.