Discussion Overview
The discussion revolves around the geometric problem of proving that angle ACB is bisected by line OC, with a focus on the construction of a circle tangent to line AB and the relationships between various points and angles in the configuration.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
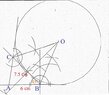
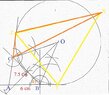
- Some participants assert that AB is 6 cm and that the circle should be tangent to AB.
- One participant mentions that AB = AC since they are tangents drawn from point A to the circle, leading to the conclusion that angles ABC and ACB are equal.
- Another participant questions how to prove that line OC bisects angle ACB, expressing doubt about the construction.
- A participant introduces a scenario involving point X outside the circle and points of tangency Y and Z, asking what can be inferred about triangles XY and XZ in relation to the circle.
- One participant suggests that the relation being sought is generally true and encourages others to make necessary corrections and apply hints provided earlier.
- A later reply discusses the congruence of triangles formed by the radius of the circle and the tangent line, suggesting this as a reason for the bisection of angle ACB.
Areas of Agreement / Disagreement
Participants express uncertainty about the construction and whether line OC indeed bisects angle ACB. There are multiple viewpoints regarding the correctness of the construction and the generality of the relationship being discussed.
Contextual Notes
Some assumptions about the construction and the properties of tangents and angles are not fully resolved, leading to varying interpretations of the problem.