Stopping the Bus in 100m - Can it be done?

[chwala]

Homework Statement

See attached.

Relevant Equations

$s$=$ut$+$\frac{1}{2}at^2$

Find the question and its solution below;

]

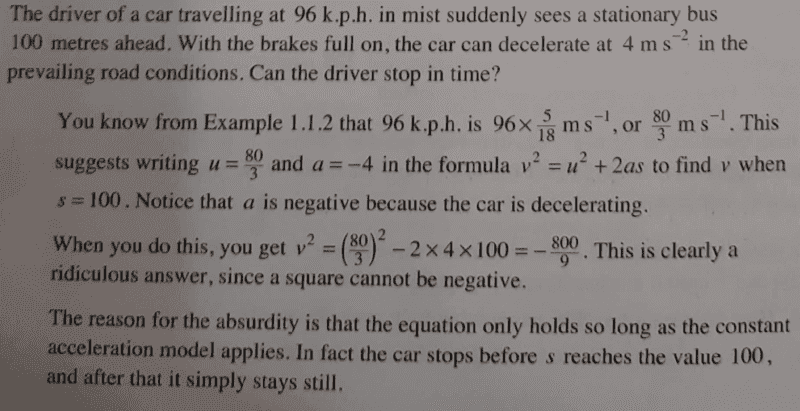Find my approach here;
The bus needs to stop at the point where, $v=0$, therefore we need to find the time taken for the car to come to a stop. using
$v=u+at$
$0=26.67 + (-4)t$
$t$=$\frac {-26.67}{-4}$=$6.6675$ seconds

The distance traveled at time, $t$=$6.6675$ is given by;
$s$=$ut$+$\frac{1}{2}at^2$
$s$=$177.822+ (-88.91)$=$88.91metres< 100 metres$

Conclusion
Yes, the driver can stop in time.

Any other way of looking at this is highly appreciated.

 

[DrClaude]

Conclusion
Yes, the driver can stop in time.

Any other way of looking at this is highly appreciated.

The other ways of looking at this are given in the solution of the textbook.

 

[robphy]

@chwala , your method is better if you want to include the driver's reaction time.
Otherwise the book's solution is more direct (assuming you know the v^2-formula)
since one doesn't have to calculate the stopping time (since no one asked about it).
If you substitute the general expression [for constant acceleration] $t=(v-u)/a$
into your $s$-equation [for constant acceleration], you'll get their $v^2$-formula [for constant acceleration]. (Try it.)

 

[chwala]

@chwala , your method is better if you want to include the driver's reaction time.
Otherwise the book's solution is more direct (assuming you know the v^2-formula)
since one doesn't have to calculate the stopping time (since no one asked about it).
If you substitute the general expression [for constant acceleration] $t=(v-u)/a$
into your $s$-equation [for constant acceleration], you'll get their $v^2$-formula [for constant acceleration]. (Try it.)

Thanks, I am conversant with the $v^2$-formula approach.

 

[chwala]

The author indicates that we ought to add $8$ to the final solution as in real life situation; it is highly unlikely to apply the brakes spontaneously after seeing the bus...it takes a few moments...

i.e even after adding;

$[8+88.91=96.91]m<100m$.