Discussion Overview
The discussion revolves around the relationships between the area and perimeter of a circle, specifically examining how the ratios of surface area to length (S/L) and their variations with radius size can be understood. The conversation touches on mathematical errors in provided tables and the implications of unit differences in these ratios.
Discussion Character
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants propose that the ratios S/L and {[S/L]/R} can vary with radius size, questioning how a circle can maintain its properties while these ratios change.
- Others argue that the ratios are not unitless, as S has units of length squared and L has units of length, leading to different behaviors when dimensions are altered.
- Several participants point out errors in the provided tables, specifically regarding the perimeter calculations and the values of S/L for certain radii.
- A participant suggests using different symbols for area and length to avoid confusion, advocating for A for area and P or C for perimeter or circumference.
- Some participants emphasize the need for correct algebraic manipulation to derive the ratios accurately, indicating that S/L simplifies to R/2 under certain conditions.
- There is a repeated assertion that S and L can numerically equal each other but differ in units, which is not clearly represented in the tables.
Areas of Agreement / Disagreement
Participants express disagreement regarding the accuracy of the tables and the interpretation of the ratios. There is no consensus on the correct values or the implications of the relationships discussed.
Contextual Notes
Limitations include potential arithmetic errors in the tables, unresolved mathematical steps in deriving the ratios, and the dependence on definitions of the symbols used for area and length.
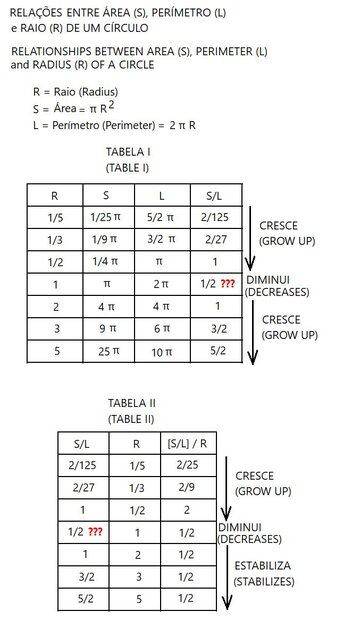
 .
.