Strange Relationships of the Circle

[dom_quixote]

PHOTOGRAPHIC REDUCTION OR ENLARGEMENT

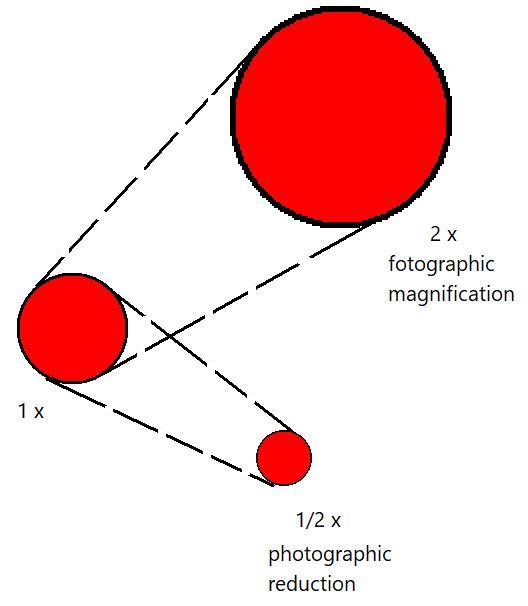
The proportions of a circle never change. But...

Question:
If a circle is always a circle, then how is it possible that the S/L and {[S/L]/R} ratios of a circle can vary as a function of the radius size?

 

[Office_Shredder]

Because they aren't unitless quantities. S has units of length squared and L has units of length, so when you double the length, they don't change the same way.

 

[jack action]

There are errors in your table for the perimeter. It should read 2/5π and 3/5π 2/3π for the first two. And S/L for R=1/2 is 1/4, not 1.

 

[hutchphd]

There are errors in your table for the perimeter. It should read 2/5π and 3/5π for the first two. And S/L for R=1/2 is 1/4, not 1.

$\frac 2 3 \pi$ ?

 

[A.T.]

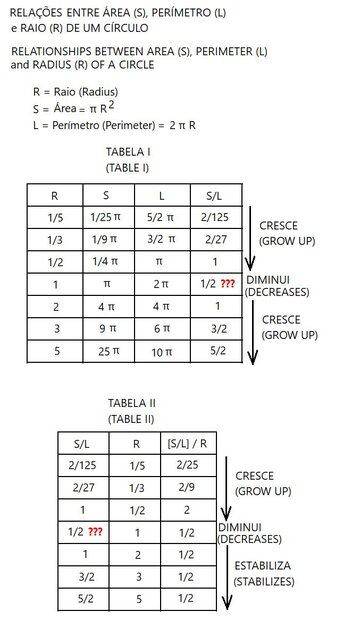
If a circle is always a circle, then how is it possible that the S/L and {[S/L]/R} ratios of a circle can vary as a function of the radius size?

Try it with a square if you have problems understanding it for a circle. It's more a geometry question rather than physics.

Related topic:
https://en.wikipedia.org/wiki/Square–cube_law

 

[The Fez]

There are many basic arithmetic errors in your charts. The [S/L]/R column should always be 1/2, for instance.

 

[dom_quixote]

In fact, I made a mistake .
The corrected table is below:

Note in the TABLE I a singularity, when R=2/1:
S = L ?
Certainly not!
S expresses area;
L expresses length.

P.S.:
If there is another error in the table, I apologize for my numerical dyslexia !

 

[DaveE]

How about applying some simple algebra before you make the tables?
Since $S=\pi R^2$ and $L=2 \pi R$ then $\frac{S}{L} = \frac{\pi R^2}{2 \pi R} = \frac{R}{2}$ and $\frac{(\frac{S}{L})}{R} = \frac{1}{2}$.
That is all there is to this, now you can correct your tables.

 

[A.T.]

S = L ?
Certainly not!
S expresses area;
L expresses length.

They can have have the same numerical value (which is what your table shows), but different units (which your table doesn't show).

If there is another error in the table, I apologize for my numerical dyslexia !

See post #6 and #8.

 

[Mark44]

Note in the TABLE I a singularity, when R=2/1:
S = L ?
Certainly not!
S expresses area;
L expresses length.

Why don't you use letters that more closely align with what they represent?
R is fine for radius, but why are you using S for area and L for length? Better would be A for area and P or C for either perimeter or circumference.

How about applying some simple algebra before you make the tables?

Or even some simple arithmetic.
You have errors in the first two rows of table 1.
$2\pi \frac 1 5 \ne \frac{5\pi} 2$
$2\pi \frac 1 3 \ne \frac{3\pi} 2$

 

[Mark44]

The initial questions have been asked and answered, so I'm closing this thread.