Stress in a tube due to external radial temperature gradiant

[LACAZE]

Hi everyone,
To begin, sorry for my english...:S

I try to calculate inner/outer surface stresses on a pipe submitted to instanatenous temperature variation on the OUTER SURFACE.

I know the Roark's formua giving the stresses but with an instantaneous temperature variation on the INNER SURFACE.

My question is: can i apply theses formulas to my case (but with a Delta T on the outer surface, not on the inner surface)?

For me, the Roark formulas is the combination result of the temperature formula on the thickness with the Hook formulas.
Temperature/thickness formula:

=>

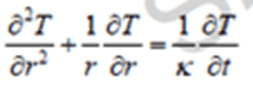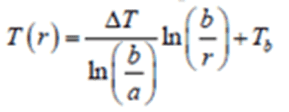
Hook formula:

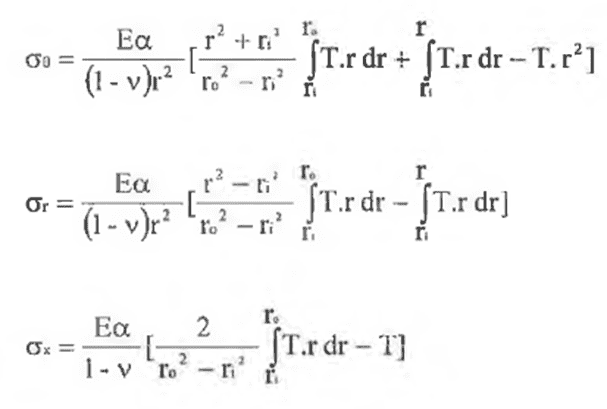So, to my mind, i can apply it to my case, it is just the results sign which change (tension stresses in outer surface area and compression stresses in inner surface area for a outer negative tempeature variation).

Thanks a lot.

Bruno.

 

[Chestermiller]

The temperature distribution in the shell is going to be a function of both time and position, not just position. For any given time you can solve for the temperature distribution within the shell by solving the transient heat conduction equation. Once you know that, you can solve the stress equilibrium equation for the stresses within the shell. You need to include the thermal expansion term in the stress equilibrium equation. The stresses will be changing as a function of time.