Jenab2
- 85
- 22
I created interpolative curvefits to the graph of Earth's density as a function of radius, shown here:
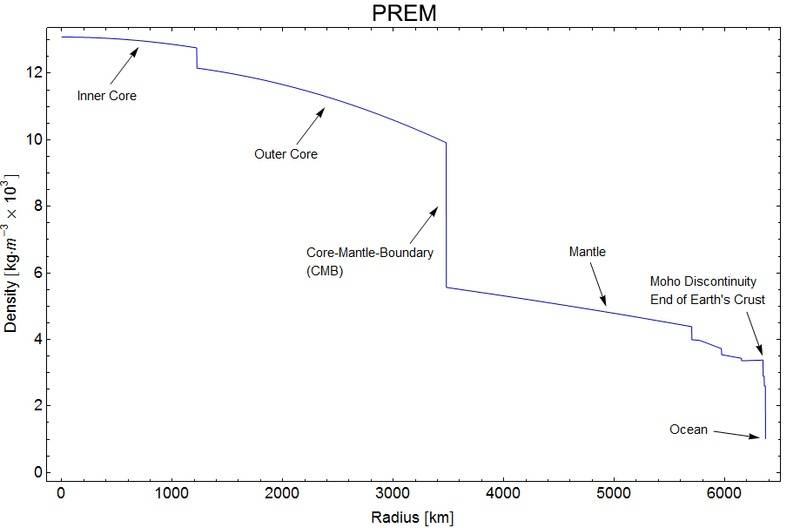
(Image from Wikipedia)
Earth is assumed to be a sphere of radius 6371 kilometers. The independent variable r is the geocentric distance as a fraction of the Earth's radius; i.e. the range of r is [0,1]. The dependent variable p is Earth's density in kilograms per cubic meter.
If 0 ≤ r < 0.1915,
ρ = −8088.796304 r² − 330.8910692 r + 13100.0
If 0.1915 ≤ r < 0.5469,
ρ = −10693.43214 r² + 1635.478802 r + 12203.95803
If 0.5469 ≤ r < 0.8947,
ρ = −3450.258769 r + 7486.946521
If 0.8947 ≤ r < 0.9953,
ρ = −6212.723658 r + 9558.523857
If 0.9953 ≤ r < 0.9992,
ρ = −102564.1026 r + 105082.0513
If 0.9992 ≤ r ≤ 1,
ρ = −125000.0 r + 126000.0
From these curvefits, the integrated mass of Earth is 5.9953e+24 kilograms, which is in excess of the experimentally measured value by 0.36%. The calculated surface gravity is 9.8579 m/sec², and the calculated average density is 5534.8 kg/m³. The relative errors are less than 1% in each case, so the equations appear to be returning a very good fit to the PREM density profile, ρ(r), of Earth's interior.
The absolute maximum for gravitational acceleration inside Earth, g(r), occurs at r=0.5470 Re (at the core-mantle boundary), enclosing 0.3259 Me, resulting in g=10.699 m/sec². There is also a local maximum for g(r) at r=0.8950 Re, enclosing 0.8179 Me, resulting in g=10.029 m/sec².
To follow is the model showing:
1. Radius fraction, r/Re
2. Enclosed mass fraction, M(r)/Me
3. Local density in kilograms per cubic meter, ρ(r)
4. Local gravitational acceleration in meters per second squared, g(r)
5. Local pressure in gigaPascals, P(r)
0.00 , 0.000000 , 13100.00 , 0.00000 , 364.8373
0.01 , 0.000002 , 13095.88 , 0.23327 , 364.7400
0.02 , 0.000019 , 13090.15 , 0.46640 , 364.4482
0.03 , 0.000064 , 13082.79 , 0.69933 , 363.9622
0.04 , 0.000152 , 13073.82 , 0.93203 , 363.2826
0.05 , 0.000296 , 13063.23 , 1.16442 , 362.4098
0.06 , 0.000512 , 13051.03 , 1.39647 , 361.3446
0.07 , 0.000812 , 13037.20 , 1.62812 , 360.0878
0.08 , 0.001211 , 13021.76 , 1.85932 , 358.6403
0.09 , 0.001723 , 13004.70 , 2.09001 , 357.0031
0.10 , 0.002362 , 12986.02 , 2.32015 , 355.1774
0.11 , 0.003141 , 12965.73 , 2.54968 , 353.1645
0.12 , 0.004073 , 12943.81 , 2.77856 , 350.9656
0.13 , 0.005173 , 12920.28 , 3.00672 , 348.5823
0.14 , 0.006453 , 12895.13 , 3.23412 , 346.0162
0.15 , 0.007927 , 12868.37 , 3.46071 , 343.2689
0.16 , 0.009607 , 12839.98 , 3.68642 , 340.3423
0.17 , 0.011507 , 12809.98 , 3.91123 , 337.2383
0.18 , 0.013639 , 12778.36 , 4.13506 , 333.9589
0.19 , 0.016016 , 12745.13 , 4.35786 , 330.5063
0.20 , 0.018541 , 12103.32 , 4.55302 , 327.0398
0.21 , 0.021305 , 12075.83 , 4.74542 , 323.4590
0.22 , 0.024338 , 12046.20 , 4.93942 , 319.7381
0.23 , 0.027651 , 12014.44 , 5.13451 , 315.8775
0.24 , 0.031256 , 11980.53 , 5.33026 , 311.8781
0.25 , 0.035162 , 11944.49 , 5.52632 , 307.7410
0.26 , 0.039381 , 11906.31 , 5.72240 , 303.4678
0.27 , 0.043922 , 11865.99 , 5.91824 , 299.0602
0.28 , 0.048795 , 11823.53 , 6.11361 , 294.5203
0.29 , 0.054010 , 11778.93 , 6.30832 , 289.8505
0.30 , 0.059575 , 11732.19 , 6.50220 , 285.0532
0.31 , 0.065500 , 11683.32 , 6.69507 , 280.1312
0.32 , 0.071793 , 11632.30 , 6.88681 , 275.0874
0.33 , 0.078461 , 11579.15 , 7.07726 , 269.9247
0.34 , 0.085514 , 11523.86 , 7.26632 , 264.6466
0.35 , 0.092957 , 11466.43 , 7.45386 , 259.2562
0.36 , 0.100797 , 11406.86 , 7.63977 , 253.7573
0.37 , 0.109042 , 11345.15 , 7.82396 , 248.1534
0.38 , 0.117696 , 11281.31 , 8.00631 , 242.4483
0.39 , 0.126766 , 11215.32 , 8.18673 , 236.6459
0.40 , 0.136256 , 11147.20 , 8.36514 , 230.7503
0.41 , 0.146171 , 11076.94 , 8.54143 , 224.7657
0.42 , 0.156515 , 11004.54 , 8.71553 , 218.6962
0.43 , 0.167291 , 10930.00 , 8.88735 , 212.5462
0.44 , 0.178502 , 10853.32 , 9.05681 , 206.3203
0.45 , 0.190151 , 10774.50 , 9.22382 , 200.0228
0.46 , 0.202239 , 10693.55 , 9.38830 , 193.6586
0.47 , 0.214768 , 10610.45 , 9.55018 , 187.2322
0.48 , 0.227738 , 10525.22 , 9.70938 , 180.7485
0.49 , 0.241150 , 10437.85 , 9.86582 , 174.2123
0.50 , 0.255003 , 10348.34 , 10.01942 , 167.6287
0.51 , 0.269295 , 10256.69 , 10.17011 , 161.0025
0.52 , 0.284025 , 10162.90 , 10.31782 , 154.3390
0.53 , 0.299191 , 10066.98 , 10.46247 , 147.6431
0.54 , 0.314789 , 9968.91 , 10.60398 , 140.9202
0.55 , 0.328639 , 5589.30 , 10.67163 , 135.0875
0.56 , 0.337975 , 5554.80 , 10.58635 , 131.3145
0.57 , 0.347591 , 5520.30 , 10.50887 , 127.5935
0.58 , 0.357488 , 5485.80 , 10.43862 , 123.9216
0.59 , 0.367668 , 5451.29 , 10.37503 , 120.2961
0.60 , 0.378133 , 5416.79 , 10.31762 , 116.7143
0.61 , 0.388884 , 5382.29 , 10.26591 , 113.1740
0.62 , 0.399922 , 5347.79 , 10.21948 , 109.6732
0.63 , 0.411248 , 5313.28 , 10.17795 , 106.2097
0.64 , 0.422864 , 5278.78 , 10.14095 , 102.7819
0.65 , 0.434771 , 5244.28 , 10.10815 , 99.3882
0.66 , 0.446970 , 5209.78 , 10.07924 , 96.0269
0.67 , 0.459461 , 5175.27 , 10.05394 , 92.6968
0.68 , 0.472244 , 5140.77 , 10.03198 , 89.3966
0.69 , 0.485322 , 5106.27 , 10.01311 , 86.1251
0.70 , 0.498693 , 5071.77 , 9.99711 , 82.8813
0.71 , 0.512358 , 5037.26 , 9.98377 , 79.6643
0.72 , 0.526318 , 5002.76 , 9.97289 , 76.4730
0.73 , 0.540573 , 4968.26 , 9.96428 , 73.3068
0.74 , 0.555122 , 4933.76 , 9.95778 , 70.1648
0.75 , 0.569966 , 4899.25 , 9.95322 , 67.0465
0.76 , 0.585103 , 4864.75 , 9.95045 , 63.9512
0.77 , 0.600535 , 4830.25 , 9.94934 , 60.8784
0.78 , 0.616259 , 4795.74 , 9.94974 , 57.8275
0.79 , 0.632277 , 4761.24 , 9.95155 , 54.7982
0.80 , 0.648587 , 4726.74 , 9.95464 , 51.7900
0.81 , 0.665188 , 4692.24 , 9.95891 , 48.8026
0.82 , 0.682079 , 4657.73 , 9.96425 , 45.8356
0.83 , 0.699259 , 4623.23 , 9.97056 , 42.8888
0.84 , 0.716728 , 4588.73 , 9.97777 , 39.9620
0.85 , 0.734484 , 4554.23 , 9.98578 , 37.0548
0.86 , 0.752525 , 4519.72 , 9.99451 , 34.1672
0.87 , 0.770850 , 4485.22 , 10.00389 , 31.2989
0.88 , 0.789458 , 4450.72 , 10.01385 , 28.4498
0.89 , 0.808346 , 4416.22 , 10.02432 , 25.6199
0.90 , 0.826568 , 3967.07 , 10.02377 , 22.9477
0.91 , 0.844103 , 3904.95 , 10.01268 , 20.4355
0.92 , 0.861745 , 3842.82 , 10.00094 , 17.9658
0.93 , 0.879486 , 3780.69 , 9.98850 , 15.5386
0.94 , 0.897317 , 3718.56 , 9.97534 , 13.1540
0.95 , 0.915229 , 3656.44 , 9.96139 , 10.8121
0.96 , 0.933214 , 3594.31 , 9.94664 , 8.5130
0.97 , 0.951264 , 3532.18 , 9.93104 , 6.2567
0.98 , 0.969368 , 3470.05 , 9.91457 , 4.0433
0.99 , 0.987517 , 3407.93 , 9.89718 , 1.8729
1.00 , 1.003515 , 1000.00 , 9.85737 , 0.0001
(Image from Wikipedia)
Earth is assumed to be a sphere of radius 6371 kilometers. The independent variable r is the geocentric distance as a fraction of the Earth's radius; i.e. the range of r is [0,1]. The dependent variable p is Earth's density in kilograms per cubic meter.
If 0 ≤ r < 0.1915,
ρ = −8088.796304 r² − 330.8910692 r + 13100.0
If 0.1915 ≤ r < 0.5469,
ρ = −10693.43214 r² + 1635.478802 r + 12203.95803
If 0.5469 ≤ r < 0.8947,
ρ = −3450.258769 r + 7486.946521
If 0.8947 ≤ r < 0.9953,
ρ = −6212.723658 r + 9558.523857
If 0.9953 ≤ r < 0.9992,
ρ = −102564.1026 r + 105082.0513
If 0.9992 ≤ r ≤ 1,
ρ = −125000.0 r + 126000.0
From these curvefits, the integrated mass of Earth is 5.9953e+24 kilograms, which is in excess of the experimentally measured value by 0.36%. The calculated surface gravity is 9.8579 m/sec², and the calculated average density is 5534.8 kg/m³. The relative errors are less than 1% in each case, so the equations appear to be returning a very good fit to the PREM density profile, ρ(r), of Earth's interior.
The absolute maximum for gravitational acceleration inside Earth, g(r), occurs at r=0.5470 Re (at the core-mantle boundary), enclosing 0.3259 Me, resulting in g=10.699 m/sec². There is also a local maximum for g(r) at r=0.8950 Re, enclosing 0.8179 Me, resulting in g=10.029 m/sec².
To follow is the model showing:
1. Radius fraction, r/Re
2. Enclosed mass fraction, M(r)/Me
3. Local density in kilograms per cubic meter, ρ(r)
4. Local gravitational acceleration in meters per second squared, g(r)
5. Local pressure in gigaPascals, P(r)
0.00 , 0.000000 , 13100.00 , 0.00000 , 364.8373
0.01 , 0.000002 , 13095.88 , 0.23327 , 364.7400
0.02 , 0.000019 , 13090.15 , 0.46640 , 364.4482
0.03 , 0.000064 , 13082.79 , 0.69933 , 363.9622
0.04 , 0.000152 , 13073.82 , 0.93203 , 363.2826
0.05 , 0.000296 , 13063.23 , 1.16442 , 362.4098
0.06 , 0.000512 , 13051.03 , 1.39647 , 361.3446
0.07 , 0.000812 , 13037.20 , 1.62812 , 360.0878
0.08 , 0.001211 , 13021.76 , 1.85932 , 358.6403
0.09 , 0.001723 , 13004.70 , 2.09001 , 357.0031
0.10 , 0.002362 , 12986.02 , 2.32015 , 355.1774
0.11 , 0.003141 , 12965.73 , 2.54968 , 353.1645
0.12 , 0.004073 , 12943.81 , 2.77856 , 350.9656
0.13 , 0.005173 , 12920.28 , 3.00672 , 348.5823
0.14 , 0.006453 , 12895.13 , 3.23412 , 346.0162
0.15 , 0.007927 , 12868.37 , 3.46071 , 343.2689
0.16 , 0.009607 , 12839.98 , 3.68642 , 340.3423
0.17 , 0.011507 , 12809.98 , 3.91123 , 337.2383
0.18 , 0.013639 , 12778.36 , 4.13506 , 333.9589
0.19 , 0.016016 , 12745.13 , 4.35786 , 330.5063
0.20 , 0.018541 , 12103.32 , 4.55302 , 327.0398
0.21 , 0.021305 , 12075.83 , 4.74542 , 323.4590
0.22 , 0.024338 , 12046.20 , 4.93942 , 319.7381
0.23 , 0.027651 , 12014.44 , 5.13451 , 315.8775
0.24 , 0.031256 , 11980.53 , 5.33026 , 311.8781
0.25 , 0.035162 , 11944.49 , 5.52632 , 307.7410
0.26 , 0.039381 , 11906.31 , 5.72240 , 303.4678
0.27 , 0.043922 , 11865.99 , 5.91824 , 299.0602
0.28 , 0.048795 , 11823.53 , 6.11361 , 294.5203
0.29 , 0.054010 , 11778.93 , 6.30832 , 289.8505
0.30 , 0.059575 , 11732.19 , 6.50220 , 285.0532
0.31 , 0.065500 , 11683.32 , 6.69507 , 280.1312
0.32 , 0.071793 , 11632.30 , 6.88681 , 275.0874
0.33 , 0.078461 , 11579.15 , 7.07726 , 269.9247
0.34 , 0.085514 , 11523.86 , 7.26632 , 264.6466
0.35 , 0.092957 , 11466.43 , 7.45386 , 259.2562
0.36 , 0.100797 , 11406.86 , 7.63977 , 253.7573
0.37 , 0.109042 , 11345.15 , 7.82396 , 248.1534
0.38 , 0.117696 , 11281.31 , 8.00631 , 242.4483
0.39 , 0.126766 , 11215.32 , 8.18673 , 236.6459
0.40 , 0.136256 , 11147.20 , 8.36514 , 230.7503
0.41 , 0.146171 , 11076.94 , 8.54143 , 224.7657
0.42 , 0.156515 , 11004.54 , 8.71553 , 218.6962
0.43 , 0.167291 , 10930.00 , 8.88735 , 212.5462
0.44 , 0.178502 , 10853.32 , 9.05681 , 206.3203
0.45 , 0.190151 , 10774.50 , 9.22382 , 200.0228
0.46 , 0.202239 , 10693.55 , 9.38830 , 193.6586
0.47 , 0.214768 , 10610.45 , 9.55018 , 187.2322
0.48 , 0.227738 , 10525.22 , 9.70938 , 180.7485
0.49 , 0.241150 , 10437.85 , 9.86582 , 174.2123
0.50 , 0.255003 , 10348.34 , 10.01942 , 167.6287
0.51 , 0.269295 , 10256.69 , 10.17011 , 161.0025
0.52 , 0.284025 , 10162.90 , 10.31782 , 154.3390
0.53 , 0.299191 , 10066.98 , 10.46247 , 147.6431
0.54 , 0.314789 , 9968.91 , 10.60398 , 140.9202
0.55 , 0.328639 , 5589.30 , 10.67163 , 135.0875
0.56 , 0.337975 , 5554.80 , 10.58635 , 131.3145
0.57 , 0.347591 , 5520.30 , 10.50887 , 127.5935
0.58 , 0.357488 , 5485.80 , 10.43862 , 123.9216
0.59 , 0.367668 , 5451.29 , 10.37503 , 120.2961
0.60 , 0.378133 , 5416.79 , 10.31762 , 116.7143
0.61 , 0.388884 , 5382.29 , 10.26591 , 113.1740
0.62 , 0.399922 , 5347.79 , 10.21948 , 109.6732
0.63 , 0.411248 , 5313.28 , 10.17795 , 106.2097
0.64 , 0.422864 , 5278.78 , 10.14095 , 102.7819
0.65 , 0.434771 , 5244.28 , 10.10815 , 99.3882
0.66 , 0.446970 , 5209.78 , 10.07924 , 96.0269
0.67 , 0.459461 , 5175.27 , 10.05394 , 92.6968
0.68 , 0.472244 , 5140.77 , 10.03198 , 89.3966
0.69 , 0.485322 , 5106.27 , 10.01311 , 86.1251
0.70 , 0.498693 , 5071.77 , 9.99711 , 82.8813
0.71 , 0.512358 , 5037.26 , 9.98377 , 79.6643
0.72 , 0.526318 , 5002.76 , 9.97289 , 76.4730
0.73 , 0.540573 , 4968.26 , 9.96428 , 73.3068
0.74 , 0.555122 , 4933.76 , 9.95778 , 70.1648
0.75 , 0.569966 , 4899.25 , 9.95322 , 67.0465
0.76 , 0.585103 , 4864.75 , 9.95045 , 63.9512
0.77 , 0.600535 , 4830.25 , 9.94934 , 60.8784
0.78 , 0.616259 , 4795.74 , 9.94974 , 57.8275
0.79 , 0.632277 , 4761.24 , 9.95155 , 54.7982
0.80 , 0.648587 , 4726.74 , 9.95464 , 51.7900
0.81 , 0.665188 , 4692.24 , 9.95891 , 48.8026
0.82 , 0.682079 , 4657.73 , 9.96425 , 45.8356
0.83 , 0.699259 , 4623.23 , 9.97056 , 42.8888
0.84 , 0.716728 , 4588.73 , 9.97777 , 39.9620
0.85 , 0.734484 , 4554.23 , 9.98578 , 37.0548
0.86 , 0.752525 , 4519.72 , 9.99451 , 34.1672
0.87 , 0.770850 , 4485.22 , 10.00389 , 31.2989
0.88 , 0.789458 , 4450.72 , 10.01385 , 28.4498
0.89 , 0.808346 , 4416.22 , 10.02432 , 25.6199
0.90 , 0.826568 , 3967.07 , 10.02377 , 22.9477
0.91 , 0.844103 , 3904.95 , 10.01268 , 20.4355
0.92 , 0.861745 , 3842.82 , 10.00094 , 17.9658
0.93 , 0.879486 , 3780.69 , 9.98850 , 15.5386
0.94 , 0.897317 , 3718.56 , 9.97534 , 13.1540
0.95 , 0.915229 , 3656.44 , 9.96139 , 10.8121
0.96 , 0.933214 , 3594.31 , 9.94664 , 8.5130
0.97 , 0.951264 , 3532.18 , 9.93104 , 6.2567
0.98 , 0.969368 , 3470.05 , 9.91457 , 4.0433
0.99 , 0.987517 , 3407.93 , 9.89718 , 1.8729
1.00 , 1.003515 , 1000.00 , 9.85737 , 0.0001
Last edited: