Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading T. S. Blyth's book "Module Theory: An Approach to Linear Algebra" ... ... and am currently focussed on Chapter 2: Submodules; Intersections and Sums ... ...
I need help with understanding two claims that Blyth makes concerning submodules ...
The relevant text is as follows: ( see end of post for other text that may be relevant)

I have two questions concerning the above text ... ...
Question 1In the above text we read:
" ... ... We know that ##A + B## is the smallest submodule of ##M## that contains both ##A## and ##B##, ... ... "My question is: how exactly do we know this ... ? How would we formally and rigorously prove this ... ?
Question 2In the above text we read:
" ... ... and that ##A \cap B## is the largest submodule contained in both ##A## and ##B##, ... ... "My question is: how exactly do we know this ... ? How would we formally and rigorously prove this ... ?Hope that someone can help with the above two questions ...
Peter
==============================================================================
PS Just in case readers need to reference some of Blyth's definitions or theorems in Chapter 2, I am providing the relevant text as follows:




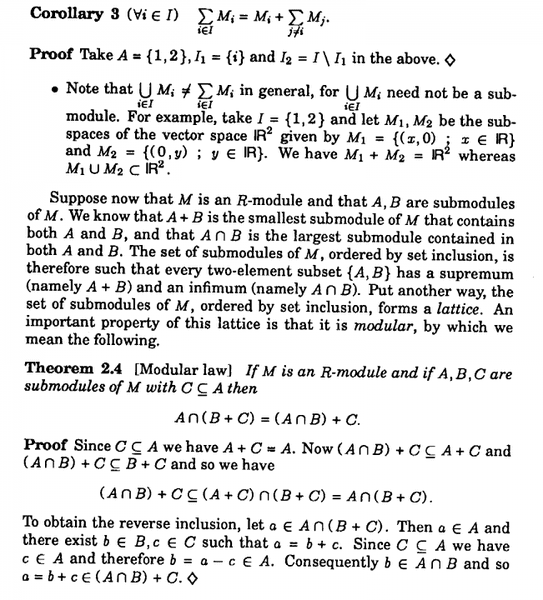
I need help with understanding two claims that Blyth makes concerning submodules ...
The relevant text is as follows: ( see end of post for other text that may be relevant)
I have two questions concerning the above text ... ...
Question 1In the above text we read:
" ... ... We know that ##A + B## is the smallest submodule of ##M## that contains both ##A## and ##B##, ... ... "My question is: how exactly do we know this ... ? How would we formally and rigorously prove this ... ?
Question 2In the above text we read:
" ... ... and that ##A \cap B## is the largest submodule contained in both ##A## and ##B##, ... ... "My question is: how exactly do we know this ... ? How would we formally and rigorously prove this ... ?Hope that someone can help with the above two questions ...
Peter
==============================================================================
PS Just in case readers need to reference some of Blyth's definitions or theorems in Chapter 2, I am providing the relevant text as follows:
Attachments
-
 Blyth - Modules ch 2 .. A plus B ... and ... A intersect B ....png40.9 KB · Views: 629
Blyth - Modules ch 2 .. A plus B ... and ... A intersect B ....png40.9 KB · Views: 629 -
 Blyth - 1 - Chapter 2 - Page 1 ... ....png39.4 KB · Views: 712
Blyth - 1 - Chapter 2 - Page 1 ... ....png39.4 KB · Views: 712 -
 Blyth - 2 - Chapter 2 - Page 2 ... ....png40.6 KB · Views: 735
Blyth - 2 - Chapter 2 - Page 2 ... ....png40.6 KB · Views: 735 -
 Blyth - 3 - Chapter 2 - Page 3 ... ....png52.9 KB · Views: 600
Blyth - 3 - Chapter 2 - Page 3 ... ....png52.9 KB · Views: 600 -
 Blyth - 4 - Chapter 2 - Page 4 ... ....png48.3 KB · Views: 636
Blyth - 4 - Chapter 2 - Page 4 ... ....png48.3 KB · Views: 636 -
 Blyth - 5 - Chapter 2 - Page 5 ... ....png67.3 KB · Views: 677
Blyth - 5 - Chapter 2 - Page 5 ... ....png67.3 KB · Views: 677