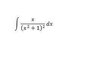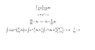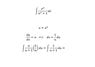Substitution Rule in Indefinite Integrals
- Thread starter phillyolly
- Start date
Click For Summary
The discussion focuses on the substitution rule in indefinite integrals, emphasizing its role as the reverse of the chain rule in differentiation. Participants share examples, demonstrating how to apply the substitution technique effectively, such as letting u = x^3 - 2 and u = sec^2(t). The importance of adjusting the integral with the correct differential, du, is highlighted, ensuring that the substitution maintains the integral's value. Additionally, alternative substitutions are explored, including one involving the exponential function, e^x. Overall, the conversation provides insights into the mechanics of the substitution rule and its practical applications in solving integrals.
Similar threads
- · Replies 3 ·
- · Replies 4 ·
- · Replies 4 ·
- · Replies 22 ·
- · Replies 2 ·