Summation Index Notation in the Transformation Equations

[sams]

In Chapter 7: Hamilton's Principle, in the Classical Dynamics of Particles and Systems book by Thornton and Marion, Fifth Edition, page 258-259, we have the following equations:

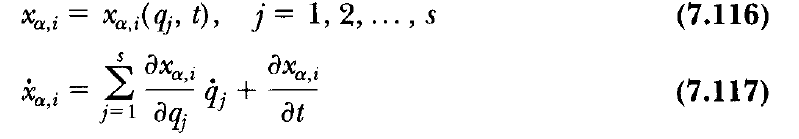
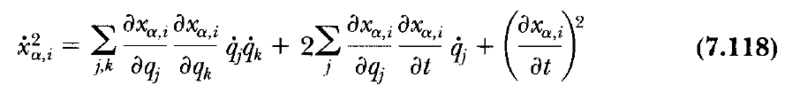
1. Upon squaring Equation (7.117), why did the authors in the first term of Equation (7.118) are summing over two indices $j$ and $k$, and not over $j$ only? In other words, where did the index $k$ come from? Why do we add sometimes a new index and when do we do that?

2. What is the physical interpretation of Equation (7.121)?

Thanks a lot!

 

[George Jones]

why did the authors in the first term of Equation (7.118) are summing over two indices $j$ and $k$, and not over $j$ only? In other words, where did the index $k$ come from? Why do we add sometimes a new index and when do we do that?

2. What is the physical interpretation of Equation (7.121)?
View attachment 232606
Thanks a lot![/QUOTE]

As easy examples, calculate
$$\sum_j q_j^2$$
and
$$\sum_{j,k} q_j q_k$$
where both $j$ and $k$ run from 1 to 3.

What is the physical interpretation of Equation (7.121)?

The physical interpretation of (7.121) is given in the words just before the equation.

 

[sams]

As easy examples, calculate
$$\sum_j q_j^2$$
and
$$\sum_{j,k} q_j q_k$$
where both $j$ and $k$ run from 1 to 3.

Thank you for your reply. Yes, I expanded the summations. The first one leads to three terms and the second one to nine terms, but I still did not get it why should we use two indices instead of one index!

 

[Carpe Physicum]

2. What is the physical interpretation of Equation (7.121)?
The physical interpretation of (7.121) is given in the words just before the equation.

For those of us who don't have the book, would you mind telling us what the words say, or showing. Thanks.

 

[sams]

For those of us who don't have the book, would you mind telling us what the words say, or showing. Thanks.