Surface area - Double integrals

[etf]

Hi!
Here is my task:
Calculate surface area of sphere $$x^{2}+y^{2}+z^{2}=16$$ between $$z=2$$ and $$z=-2\sqrt{3}$$.
Here are 3D graphs of our surfaces:

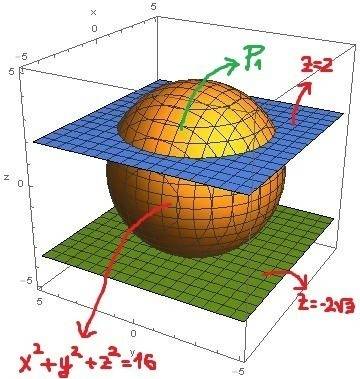
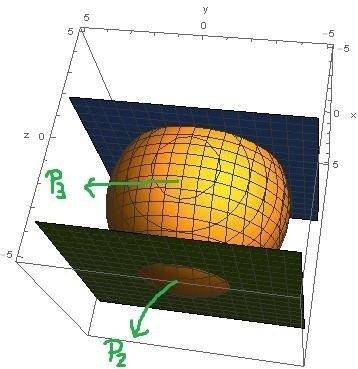
Surface area of interest is P3. It would be P-(P1+P2), where P is surface area of whole sphere. Is it correct?
Here is how I calculated P1:

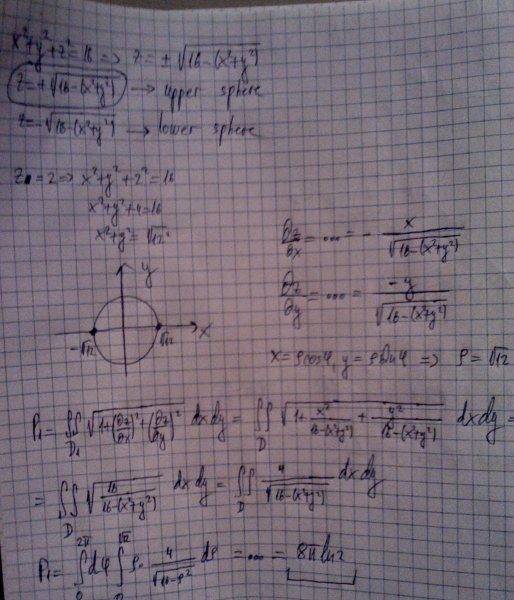
Similarly for P2:

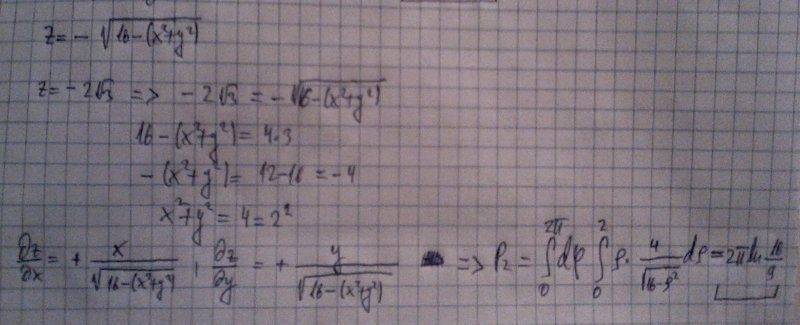
We calculate P using formula 4pi*r*r.
Is it correct?

 

[SteamKing]

Can't really decipher your answer. It looks like 2πscribble.

 

[etf]

P1=8*pi*ln2, P2=2*pi*ln(16/9), P=4*pi*16
P=4*pi*16-(8*pi*ln2+2*pi*ln(16/9))=201.0619-21.0358=180.0261

 

[SteamKing]

P1=8*pi*ln2, P2=2*pi*ln(16/9), P=4*pi*16
P=4*pi*16-(8*pi*ln2+2*pi*ln(16/9))=201.0619-21.0358=180.0261

You can check your result using the formula in this article:

http://en.wikipedia.org/wiki/Spherical_segment

It seems there is a disagreement somewhere in your calculations between the formula and your result.

 

[LCKurtz]

etf, have you given any consideration to working the problem in spherical coordinates? You can calculate it directly in about two steps.

 

[etf]

I'm not familiar with spherical coordinates :(

 

[SteamKing]

I'm not familiar with spherical coordinates :(

It's like polar coordinates, but with an extra angular coordinate:

http://en.wikipedia.org/wiki/Spherical_coordinate_system

 

[STEMucator]

Doing multiple integrals and not being familiar with integral transforms is not a good thing. Polar, spherical and cylindrical co-ordinates are important to be able to integrate properly, and without them, you won't get very far.

An interesting way to do this problem is to describe each face of the surface and then perform a surface integral over each one:

$$\iint_S \space dS = \iint_{S_1} \space dS_1 + \iint_{S_2} \space dS_2 + \iint_{S_3} \space dS_3$$

So you have a flat top surface $S_1$ described by the plane $z = 2$ and bounded by the region $D_1$ given by $x^2 + y^2 = 12$. You also have a flat bottom surface $S_2$ describe by the plane $z = -2 \sqrt{3}$ and bounded by the region $D_2$. Finally, you have the spherical middle section bounded by the planes.

 

[SteamKing]

Doing multiple integrals and not being familiar with integral transforms is not a good thing. Polar, spherical and cylindrical co-ordinates are important to be able to integrate properly, and without them, you won't get very far.

An interesting way to do this problem is to describe each face of the surface and then perform a surface integral over each one:

$$\iint_S \space dS = \iint_{S_1} \space dS_1 + \iint_{S_2} \space dS_2 + \iint_{S_3} \space dS_3$$

So you have a flat top surface $S_1$ described by the plane $z = 2$ and bounded by the region $D_1$ given by $x^2 + y^2 = 12$. You also have a flat bottom surface $S_2$ describe by the plane $z = -2 \sqrt{3}$ and bounded by the region $D_2$. Finally, you have the spherical middle section bounded by the planes.

I think the OP was supposed to calculate only the area of the spherical surface lying between the planes z = -2√3 and z = 2. I don't think the areas of S₁ or S₂ were ever intended to be included.

 

[STEMucator]

I think the OP was supposed to calculate only the area of the spherical surface lying between the planes z = -2√3 and z = 2. I don't think the areas of S₁ or S₂ were ever intended to be included.

Sorry, I saw the problem a little differently when I first read it this morning. The sphere with its ends cut off seems to be more appropriate, so the $dS_3$ integral would be the only thing required. I believe the conventional method of evaluation then proceeds as usual:

$$\iint_S \space dS = \iint_D \sqrt{z_x^2 + z_y^2 + 1} \space dA$$

The two planes and sphere give two circles in the x-y plane from which the limits can be deduced.

 

[LCKurtz]

Sorry, I saw the problem a little differently when I first read it this morning. The sphere with its ends cut off seems to be more appropriate, so the $dS_3$ integral would be the only thing required. I believe the conventional method of evaluation then proceeds as usual:

$$\iint_S \space dS = \iint_D \sqrt{z_x^2 + z_y^2 + 1} \space dA$$

The two planes and sphere give two circles in the x-y plane from which the limits can be deduced.

That is certainly not the "natural" method to use. The surface is not symmetric vertically so you would have to work the top and bottom portions separately. And rectangular coordinates also are not the natural choice.