Swimming Pools and Related Rates along with Implicit Differentiation

[Salazar]

Homework Statement

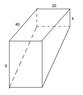
A swimming pool is 40 feet long, 20 feet wide, 4 feet deep at the shallow end, and 9 feet deep at the deep end. Water is being pumped into the pool at 10 cubic feet per minute.
a. When the water is 3 feet deep at the shallow end, at what rate is the water level rising? b. When the water is 3 feet deep at the deep end, at what rate is the water level rising?

Homework Equations

None Given.

The Attempt at a Solution

I had [dV/dt] and the volume for part a is V = L*W*H and I had L and W, which were 40' and 20' respectively. So V = 800H and I used implicit differentiation to get [dV/dt] = 800[dH/dt], so [dH/dt] = 1/80 feet per minute.

For part be it seems straightforward, but I do not know how to get the length, since it has change. Picture of the pool is uploaded.

 

[clamtrox]

Counting h from the top of the pool you have then
V = LWH for 0 < H < 4 ft and
V = something else for 4 ft < H < 9ft.

 

[Salazar]

I understand that, but what is such something else for L, length?

 

[clamtrox]

The volume of the lower half is a triangles area times the width of the pool; you can give the triangle for example by one of the angles and the height, you do not need to use length explicitly at all.